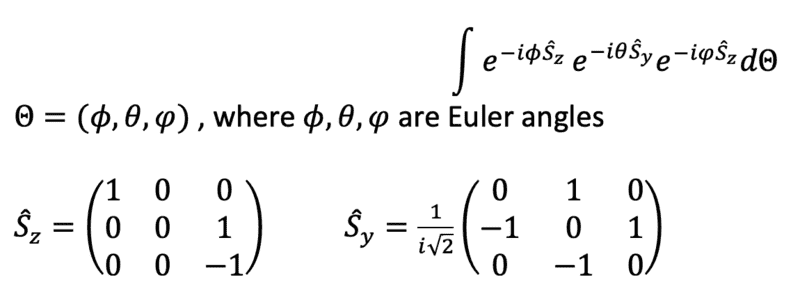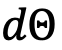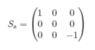The discussion centers on the challenges of integrating exponential matrices related to Euler angles and their implications in quantum mechanics. Participants identify issues with the determinant of matrices representing spin operators, noting that both matrices have a determinant and trace equal to zero. This leads to the conclusion that the rotations are non-invertible when applied to spin states. One participant expresses confusion about how to properly derive the Euler angle vector for integration. The conversation highlights the intersection of quantum mechanics and coordinate transformations, emphasizing the complexities involved in these mathematical representations.
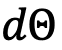 in terms those three Euler angles.
in terms those three Euler angles.