garthenar
- 35
- 8
- Homework Statement
- Two slits spaced 0.0720 mm apart are 0.800 m from a screen. Coherent light of wavelength λ passes through the two slits. In their interference pattern on the screen, the distance from the center of the central maximum to the first minimum is 3.00 mm. The intensity at the peak of the central maximum is 0.0900 W/m2.
a) What is the intensity at point on the screen that is 2.00 mm from the center of the central maximum?
b) What is the intensity at point on the screen that is 1.50 mm from the center of the central maximum?
- Relevant Equations
- λ=(ax)/D
a = distance between the two slits
x = the distance between maximums
m = which maximum your looking at (from the center)
D = the distance between the "source" (slits) and the screen
path difference
Δp = asin(θ)
= atan(θ)
= (ay/D)
y = vertical distance
phase difference
Φ = Δp (2π / λ)
= Δp k
I = 4(I_0)cos^2(Φ/2)
I'm still on part a.
I think that i may have the wrong equation for intensity.
I'm not sure I'm using the right numbers for the "first minimum".
I started with getting the wavelength
λ=(ax)/D
since the first minimum occurs at m = 0.5 I multiplied the distance to the first minimum by 2 to get the distance to the first "fringe". (point of maximum constructive interference)
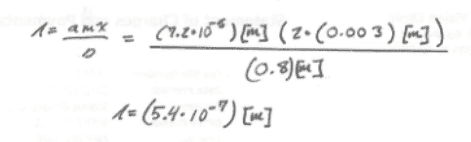
I then got the path difference
Δp = (ay/D)
I used the distance to the point I want the intensity at for y

Then the phase difference
Φ = Δp (2π / λ)
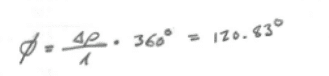
And finally my intensity
I = 4(I_0)cos^2(Φ/2)
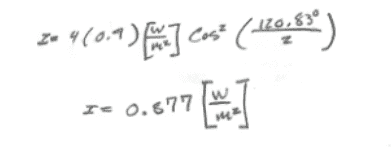
Which was wrong.
Can you help me figure out where I went wrong. I've tried several variation on this.
Thank you
I think that i may have the wrong equation for intensity.
I'm not sure I'm using the right numbers for the "first minimum".
I started with getting the wavelength
λ=(ax)/D
since the first minimum occurs at m = 0.5 I multiplied the distance to the first minimum by 2 to get the distance to the first "fringe". (point of maximum constructive interference)
I then got the path difference
Δp = (ay/D)
I used the distance to the point I want the intensity at for y
Then the phase difference
Φ = Δp (2π / λ)
And finally my intensity
I = 4(I_0)cos^2(Φ/2)
Which was wrong.
Can you help me figure out where I went wrong. I've tried several variation on this.
Thank you