Intro Physics homework help - distance and velocity

In summary, the person had trouble getting the correct answer for a problem and asked for help. Another person pointed out that they were calculating the area of the wrong velocity-time graph and showed them how to calculate it correctly. The person then realized their mistake and thanked the other person.
  • #1
mncyapntsi
38
4
Homework Statement
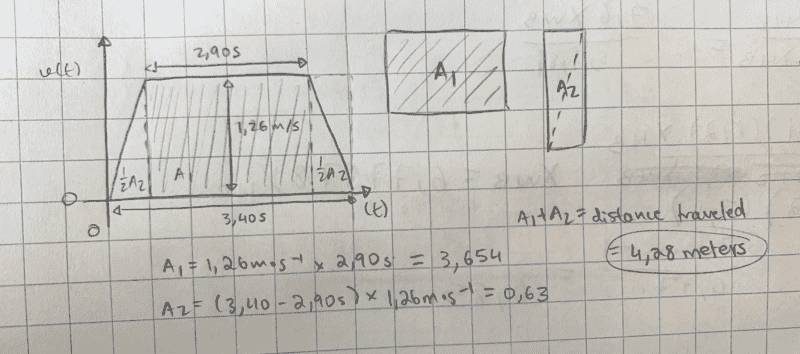
An elevator going up from one floor to the next, where velocity is positive if it is upward. The acceleration at the start and the deceleration at the end are uniform and of the same magnitude. If the maximum speed of the elevator is 1.26 m/s and it takes a total of 3.40 s for the elevator to move between the floors, what is the distance between the floors if the time that the elevator maintains its top speed is 2.90 s?
Relevant Equations
v=d/t ; x = xo + vt
I have tried this problem over 4 times and keep getting the exact same answer, which is incorrect. Could someone please help by pointing out what I did wrong, or letting me know if I am actually on the completely wrong path?
Thanks!
Have a wonderful day :)
Screen Shot 2021-09-14 at 2.59.30 PM 1.png
 
Physics news on Phys.org
  • #2
Is the answer supposed to be ##3.97m##?
 
  • #3
PeroK said:
Is the answer supposed to be ##3.97m##?
Could I please ask how you got that?
 
  • #4
mncyapntsi said:
Could I please ask how you got that?
I calculated the area of your velocity-time graph. Whereas, you calculated the area of a velocity-time graph for a speed of ##1.26 m/s## for the full ##3.4s##.
 
  • #5
OH! I see what I did - thanks a lot!
 

1. What is the difference between distance and displacement?

Distance is the total length traveled by an object, while displacement is the shortest distance between the starting and ending points.

2. How do you calculate average velocity?

Average velocity is calculated by dividing the total displacement by the total time taken.

3. What is the difference between average velocity and instantaneous velocity?

Average velocity is the average rate of change of an object's position over a specific period of time, while instantaneous velocity is the velocity of an object at a specific moment in time.

4. How does acceleration affect an object's velocity?

Acceleration is the rate of change of an object's velocity. If an object is accelerating, its velocity will change by a certain amount over a specific period of time.

5. How do you calculate the final velocity of an object?

The final velocity of an object can be calculated using the initial velocity, acceleration, and time. The formula is Vf = Vi + at, where Vf is the final velocity, Vi is the initial velocity, a is the acceleration, and t is the time.

Similar threads

Measuring the Velocity of Sound in this Lab Exercise
    • Introductory Physics Homework Help
Replies
19
Views
453
Calculate Distance Traveled: Instantaneous vs. Average Velocity
    • Introductory Physics Homework Help
Replies
5
Views
1K
Solving Distance Traveled Using Formulas vs. Graphs
    • Introductory Physics Homework Help
Replies
6
Views
785
Calculating Velocity Vector of Object in 2D Space
    • Introductory Physics Homework Help
Replies
10
Views
1K
Find minimum stopping distance
    • Introductory Physics Homework Help
Replies
3
Views
3K
Intro Physics projectile problem: Archer fish and grasshopper
    • Introductory Physics Homework Help
Replies
6
Views
3K
Braking speed and distance traveled
    • Introductory Physics Homework Help
Replies
12
Views
2K
Intro to probability density QM
    • Introductory Physics Homework Help
Replies
6
Views
1K
Magnitude of an electric field
    • Introductory Physics Homework Help
Replies
4
Views
2K
Not exactly a homework issue - just trying to find a formula
    • Introductory Physics Homework Help
Replies
8
Views
1K

Hot Threads

Recent Insights

Back
Top