Introduction to Simple Matrix Rings in Noncommutative Algebra

[Math Amateur]

I am reading Matej Bresar's book, "Introduction to Noncommutative Algebra" and am currently focussed on Chapter 1: Finite Dimensional Division Algebras ... ...

I need help with some aspects of Bresar's Example 1.10 on a simple matrix ring over a division ring ...

Example 1.10, including some preamble, reads as follows:

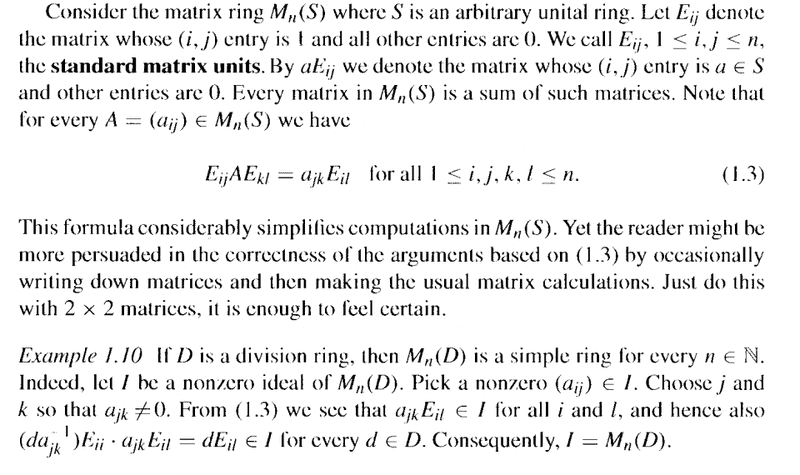In the above text from Bresar we read the following:

" ... and hence also $(d a_{jk}^{-1} ) E_{ii} \cdot a_{jk} E_{il} = d E_{il} \in I$ for every $d \in D$. Consequently, $I = M_n(D)$. ... ... "My questions are as follows:Question 1I am assuming that $(d a_{jk}^{-1} ) E_{ii} \cdot a_{jk} E_{il} = d E_{il}$ because you can take the "scalars" out of the multiplication and multiply them as in

$c_1 (a_{ij} ) \cdot c_2 (b_{ij} ) = c_1 c_2 (a_{ij} ) \cdot (b_{ij} )$Is that correct?(Note: why we are messing with multiplications by scalars in a problem on rings, I don't know ... we seem to be treating the ring $M_n (D)$ as an algebra over $D$ ... )

Question 2Bresar seems to be assuming that $d E_{il} \in I$ for all $1 \le i, l \le n$ and for every $d \in D$ implies that $I = M_n (D)$ ...

But ... ... why exactly is this true ...My thoughts ... maybe it is true because the $E_{il}$ generate the ring $M_n (D)$ ... or to put it another way ... any element in $I$ or $M_n (D)$ can be written uniquely in the form $\sum_{i, j = 1}^n d_{ij} E_{ij}$ ...and further, that all the $E_{ij}$ belong to I ...Help with these questions will be appreciated ...

Peter==============================================================================

So that readers of the above post can appreciate the relevant context of the post, I am providing the introduction to Section 1.3 Simple Rings ... as follows:

 

[fresh_42]

Question 1
I am assuming that $(d a_{jk}^{-1} ) E_{ii} \cdot a_{jk} E_{il} = d E_{il}$ because you can take the "scalars" out of the multiplication and multiply them as in
$c_1 (a_{ij} ) \cdot c_2 (b_{ij} ) = c_1 c_2 (a_{ij} ) \cdot (b_{ij} )$
Is that correct?

Yes.

(Note: why we are messing with multiplications by scalars in a problem on rings, I don't know ... we seem to be treating the ring $M_n (D)$ as an algebra over $D$ ... )

Yes. If you consider $(n \times n)-$matrix multiplication then it is defined with $n$ scalar multiplications in $n^2$ positions - a total of $n^3$ scalar multiplications (*). Therefore it is essential how scalars multiply with each other. Imagine our scalar multiplication was defined by $a\cdot a=0$ for all scalar $a$. We'd get a pretty different matrix ring. (I didn't write $a \in D$ for it would have suggested $D$ to be a division ring, which can't be with such a definition of multiplication. Therefore I simply wrote "scalar $a$".)

Question 2
Bresar seems to be assuming that $d E_{il} \in I$ for all $1 \le i, l \le n$ and for every $d \in D$ implies that $I = M_n (D)$ ...
But ... ... why exactly is this true ...

With $dE_{il} \in I$ we have all scalar multiples in $I$, esp. $d^{-1}(dE_{il})=E_{il}$ and all of them, i.e. the entire basis or $M_n(D)=\sum_{ij}a_{ij}E_{ij} \subseteq \sum D\cdot I \subseteq I \subseteq M_n(D)$.

My thoughts ... maybe it is true because the $E_{il}$ generate the ring $M_n (D)$ ... or to put it another way ... any element in $I$ or $M_n (D)$ can be written uniquely in the form $\sum_{i, j = 1}^n d_{ij} E_{ij}$ ...and further, that all the $E_{ij}$ belong to I ...

Yes.

(*) I know it can be done with less than $n^3$ and that the current record holder is est. $\omega = 2.37_3$.