elecboss
- 1
- 0
Hi good day. I am trying to find the general Inverted Pendulum on a cart nonlinear state space equations with two degrees of freedom with x, x_dot, theta, theta_dot which represents displacement, velocity, pendulum angle from vertical, angular velocity. However from research, I am seeing different state space equations. In the image attached is Matlab code I found that gives the proper functionality but I am not sure how it was derived.
y-state
m-mass of the pendulum
M- mass of the cart
L- length of pendulum line
g- gravity
d- friction
u- force on cart
The other image shows the closest set of equations I found but I am unsure. Please help thank you.

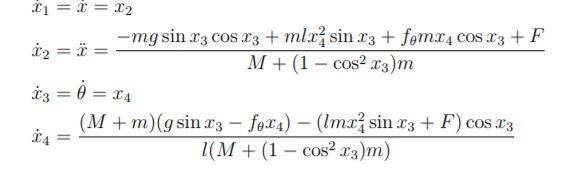
y-state
m-mass of the pendulum
M- mass of the cart
L- length of pendulum line
g- gravity
d- friction
u- force on cart
The other image shows the closest set of equations I found but I am unsure. Please help thank you.