An Example of Servo-Constraints in Mechanics

Servo-constraint was invented by Henri Beghin in his Ph.D. thesis in 1922. For details see the celebrated monograph in rational mechanics by Paul Appell.

To understand what this is, we consider the following example.

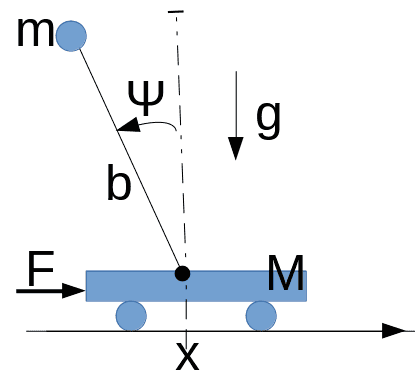
A trolley of mass $M$ can move freely along the horizontal ground in the standard gravity field. A pendulum is placed on the trolley. The pendulum consists of a massless rod of length $b$ and a mass point $m$. The position of the system is described by the generalized coordinates $x,\psi$. Where $x$ is a horizontal coordinate of the pendulum’s pivot (see the picture).

A horizontal force $\boldsymbol F=F\boldsymbol e_x$ applied to the trolley provides fulfillment of the equality $$\dot x+a\dot\psi=0,\qquad (1)$$ here $a\ne 0$ is a constant. So equation (1) determines a servo-constraint.

Let us discuss the statement of our problem. The first question is: is such a statement correct? In other words, can equality (1) be provided by such a force $\boldsymbol F$? And the second question is: does (1) determine an ideal constraint?

To answer these questions let us forget about constraint (1) for a while and assume that just some force $\boldsymbol F$ is applied to the trolley.
Then the equations of motion are
$$\frac{d}{dt}\frac{\partial L}{\partial \dot x}-\frac{\partial L}{\partial x}=F,\quad \frac{d}{dt}\frac{\partial L}{\partial \dot \psi}-\frac{\partial L}{\partial \psi}=0,\qquad( 2)$$
where
$$L=\frac{m}{2}\Big(\dot x^2+b^2\dot\psi^2-2\dot x\dot\psi b\cos\psi\Big)+\frac{M}{2}\dot x^2-mgb\cos\psi.$$
To avoid long formulas we present a scheme of the argument. Equations (2) can be written in the form
$$\ddot x=u(x,\psi,\dot x,\dot \psi,F),\quad \ddot\psi =v(x,\psi,\dot x,\dot \psi,F).\qquad (3)$$
Now differentiate equality (1):
$$\ddot x+a\ddot \psi=0 \qquad (4)$$ and substitute here formulas (3) to get
$$u(x,\psi,\dot x,\dot \psi,F)+a v(x,\psi,\dot x,\dot \psi,F)=0.\qquad (5)$$
It turns out that the function $F=F(x,\psi,\dot x,\dot \psi)$ is uniquely determined by equations (5) provided
$$b+a\cos\psi\ne 0.$$
Summarize our results. Assume that the last inequality is fulfilled and the function $F=F(x,\psi,\dot x,\dot \psi)$ is defined as above, then the function $f= \dot x+a\dot\psi$ is a first integral of equations (2). Particularly, if initial conditions satisfy (1) then (1) will be satisfied for all time till the solution exists.

This gives positive answer to the first question. The answer to the second question is negative: $F\delta x\ne 0\quad (\delta x+a\delta\psi=0)$ since $F\ne 0$. Moreover, in case of ideal constraints equations of motion have well-known form:

$$\frac{d}{dt}\frac{\partial L}{\partial \dot x}-\frac{\partial L}{\partial x}=\lambda,\quad \frac{d}{dt}\frac{\partial L}{\partial \dot \psi}-\frac{\partial L}{\partial \psi}=a\lambda.$$

Compare it with (2).

Discuss briefly dynamics of this system. The second equation of system (2) has the form
$$b\ddot\psi-\ddot x\cos\psi-g\sin\psi=0.$$
Substitute here $\ddot x$ from (4) to have
$$\ddot\psi-\frac{g\sin\psi}{b+a\cos\psi}=0.\qquad (6)$$
This system has a weird first integral of energy type
$$\frac{1}{2}\dot\psi^2+\frac{g}{a}\log\Big|\frac{b}{a}+\cos\psi\Big|=h.$$
From (6) we deduce that if $b+a<0$ then upper vertical equilibrium $\psi=0$ is stable.