Is 1.977x10^-19 J the Change in Energy in the Bohr Model?

[RJLiberator]

Okay, I am in need of some guidance:

7)Calculate the wavelength that corresponds to an emission of energy of 1.977x10^-19 J.

Okay, well here is my thought process initially: Change in Energy = hc/wavelength.

First question: Is 1.977*10^-19 THE change in energy? OR is that the Energy FINAL and the Energy initial is some constant that I SHOULD know already?

If it is the CHANGE in energy then using the equation I can get the wavelength rather easy by simply plugging in Planck's constant and the speed of light. My answer was 1005 nm doing this process.

My question to YOU is is this correct? OR am I missing the initial energy, and if so, where can I find this 'initial energy?'

Next,
8)If the initial energy level for the energy change in problem seven is n = 7, what is the final energy level?

Uhhh.. how do I find this? Any leads on this? I feel like I am missing some chart of numbers that corresponds the energy changes to certain "n" levels.

And finally,

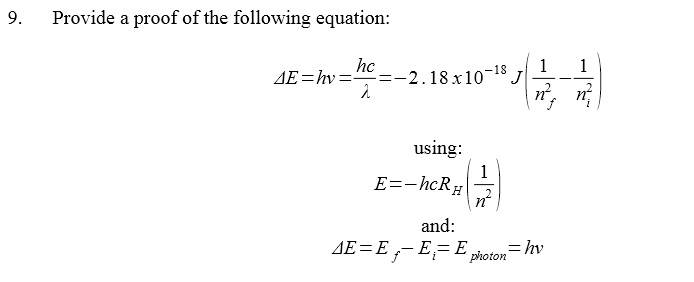
Any leads, websites, directions I can check out to get me started here?

Thanks all for your help.

 

[Matterwave]

7) By the way the question is worded, the energy given should be the energy of the emitted photon (light) and so with your terminology, specifically for the Bohr atom, would be the change in energy.

8) If your initial energy is X and your change in energy is Y, then what's your final energy? What energy level does this correspond to?

 

[maajdl]

Well, sure, for 7: "an emission of energy", sure that means the energy taken away by the photon.
Why would you need to know more: you have a photon and its energy.
Forget about these states, that doesn't make sense.

For 8: Ei-Ef = DE, and Ei=E(n=7) . The problem is: there is no indication about which atom is involved.
For hydrogen, have a look at wikipedia (http://en.wikipedia.org/wiki/Hydrogen_atom).
You should know the level of hydrogen: En = -Rydberg/n² where Rydberg = 13.6 eV

For 9: So trivial that the difficulty is to understand why they ask.

 

[RJLiberator]

Thanks guys for the posts.

So it seems on Question 7) My assumption was correct with the wording that the change in energy was what was giving. This is excellent, that problem is solved and I feel great about it.

For question 8) I'm not quite sure how to find the initial energy. Is the initial energy = to 13.6 eV ?

As far as Question 9 goes... Trivial... maybe, but I'd like to understand it =).

 

[Borek]

9. Express the E_i and E_f using equation for energy that they supplied (the middle one).

 

[maajdl]

read http://en.wikipedia.org/wiki/Hydrogen_atom

 

[RJLiberator]

I'm sorry guys, I'm having a hard time with number 8.

I keep reading the wikipedia article and my notes, but keep coming up with loose theories on what to do and I'm not too confident in it.

So, let me think about this situation here.

We have a energy change of 1.977 * 10^-19 J.
We have the initial Energy level of n = 7.
From question 7, I've found the wavelength to be 1005 nm.

So what piece of information tells me whether the emission of energy in it's initial state was lower then n=7 or higher than n=7?

Is it this equation that I keep looking at:
(1/initial n^2 - 1/final n^2)

Under this scenario, initial n^2 would be 7^2 or 49.
But where the hell do you find initial n from :O. There's got to be some equation that I am simply missing or some constant that I do not have.

I will continue to read my book now, but if anyone can lead me further I would be greatful :D

 

[RJLiberator]

Oh, and can anyone confirm my answer to 7 is correct ?

What I did was the following:

Wavelength = hc/Change in energy.

wavelength = ((6.626068*10^-34)(2.998*10^8))/(1.977*10^-19)
Which gave me 1005 nm.

 

[RJLiberator]

I think I may have made a breakthrough.

So we know that the energy is 1.997*10^-19 J we will call this "E" for simplicity.

If I throw that piece of information in an equation : E = E(1/ni^2) where n initial = 7. Then we have E*(1/49) Which will be the n=7 level.

Great.

Now I need E*(1/nfinal^2) But how do I find this n'final number that I am looking for.

From these equations I can find out if the change in level caused an electron to be absorbed or emitted!

 

[Borek]

Solve 9 first. Once you will know the equation is correct, just plug everything into it and solve for n_f. Pure (and quite simple) algebra.

 

[RJLiberator]

okay, here is what I am doing:

Ephoton = Change in Energy = Efinal-Einitial=plancks constant * frequency.

So what I did was, I used the wavelength I got in Question 7 which was 1005 and plugged that into find the frequency. The frequency was 2.9831*10^14.

I multiplied that frequency with Plancks constant to receive Ephoton which was 1.9766*10^-19.

I then used my earlier understanding of 1.977*10^-19* (1/49) to find Einitial.

I added Einitial to the Energy final to receive the total of Efinal which came out to be 2.016947*10^-19.

These answers make sense to me. I guess I have to find out the final energy level now by:
1.977*10^-19(1/n^2)=2.016947*10^-19

Based on this, the final N level is 1.
So the energy change went from n=7 to n=1. Does this sound proper?

 

[RJLiberator]

Can anyone confirm that I am on the correct path?