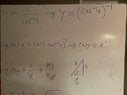Discussion Overview
The discussion revolves around the relationship between the arcsecant and arccosine functions, specifically whether arcsec(x) is equal to 1/arccos(x). Participants explore this concept through various mathematical approaches, including the use of triangles and derivatives, while also addressing potential misunderstandings about reciprocal and inverse functions.
Discussion Character
- Exploratory
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
- Some participants express confusion about the meaning of 1/arccos and its relationship to arcsec.
- Others suggest checking values using a calculator to see if arcsec(x) equals 1/arccos(x) for specific angles.
- There is a discussion about the distinction between reciprocal and inverse functions, with some arguing that they do not equate.
- One participant proposes that arcsec(1/x) might equal 1/arccos(x), prompting further exploration of this relationship.
- Concerns are raised about the domains of the functions, with some noting that they do not match, which could imply they are not the same function.
- Participants discuss the process of finding derivatives of inverse trigonometric functions and the challenges of using triangles to visualize these relationships.
- There are claims that the derivative of 1/arccos(x) leads to confusion, with some participants suggesting that it results in an incorrect expression.
Areas of Agreement / Disagreement
Participants do not reach a consensus on whether arcsec(x) equals 1/arccos(x). There are multiple competing views, with some asserting they are different functions while others explore potential relationships.
Contextual Notes
Limitations include unresolved mathematical steps regarding the derivatives and the specific conditions under which the functions are defined. Additionally, there is uncertainty about the correct application of trigonometric identities and their implications.