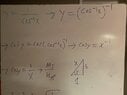Is arcsec = 1 divided by arccos ? Arcsec = 1/arccos

[Vividly]

TL;DR Summary

Im confused about what 1/arccos is equal too.

Im not sure what 1/arccos is. I looked online and all I have found is y=arccos(1/x) and I am not sure if that's the same thing. I tried to make a triangle to decipher the answer. However when I looked at the answer when I finished it was incorrect. I got 1/xsqrt(x^2-1) and the answer is 1/(arccos)^2 sqrt(1-x^2)

 

[PeroK]

You could try putting some angles into a calculator or spreadsheet and checking whether $arcsec \ x = \frac 1 {\arccos x}$.

Alternatively, if we let $y = \arccos x$ and $z = arcsec \ x$, then $\sec z = x$ ... Can you finish it from there?

 

[anuttarasammyak]

You seem to confuse reciprocal and inverse function. Say
$$y=\frac{1}{\arccos x}$$,
$$x=\cos(\frac{1}{y})$$
Say
$$y=arccos(\frac{1}{x})$$
$$x=\frac{1}{\cos y}$$

 

[Vividly]

You could try putting some angles into a calculator or spreadsheet and checking whether $arcsec \ x = \frac 1 {\arccos x}$.

Alternatively, if we let $y = \arccos x$ and $z = arcsec \ x$, then $\sec z = x$ ... Can you finish it from there?

I am confused about why you have all those number signs. Is it for a formula in excel? If your say that z=arcsec divided by x is equal to some number or 1/secz=x then x = cosz

 

[Vividly]

You seem to confuse reciprocal and inverse function. Say
$$y=\frac{1}{\arccos x}$$,
$$x=\cos(\frac{1}{y})$$

Are you saying reciporal and inverse functions do not equate to one another? So 1/arccos(x)≠ arcsec(x) ?

 

[PeroK]

I am confused about why you have all those number signs. Is it for a formula in excel? If your say that z=arcsec divided by x is equal to some number or 1/secz=x then x = cosz

What's a "number sign"? You mean variables $y, z$?

You do understand that IF $arcsec \ x = \frac 1 {\arccos x}$, then this is true for any angle $x$?

That means that:

$arcsec \ 0.1 = \frac 1 {\arccos 0.1}$

$arcsec \ 0.5 = \frac 1 {\arccos 0.5}$

$arcsec \ 1.0 = \frac 1 {\arccos 1.0}$

Etc. Did you try those on a calculater to see whether they really are equal?

 

[Vividly]

If you’re saying that z=arcsec divided by x is equal to some number or 1/secz=x then x = cosz

 

[anuttarasammyak]

So 1/arccos(x)≠ arcsec(x) ?

I am not used to arcsec function in RHS. I assume it means
$$x=\sec y = \frac{1}{\cos y}$$ right ?

LHS function means
$$x=cos(\frac{1}{y})$$

They are different functions.

 

[Vividly]

What's a "number sign"? You mean variables $y, z$?

You do understand that IF $arcsec \ x = \frac 1 {\arccos x}$, then this is true for any angle $x$?

That means that:

$arcsec \ 0.1 = \frac 1 {\arccos 0.1}$

$arcsec \ 0.5 = \frac 1 {\arccos 0.5}$

$arcsec \ 1.0 = \frac 1 {\arccos 1.0}$

Etc. Did you try those on a calculater to see whether they really are equal?

Arcsec(0.1) =error
I/arccos(0.1)=.6799811946

with that being said they’re not the same. So inverse trig functions have no relation, well at least in this regard. So how can I solve the problem? I don’t understand how to make it possible. I can try the quotient rule but not sure if that will work.

 

[PeroK]

Arcsec(0.1) =error
I/arccos(0.1)=.6799811946

So, they don't even have the same domain. Not much chance of being the same function then.

 

[PeroK]

What about? $$arcsec(\frac 1 x) = \frac{1} {\arccos x}$$Does that look better?

 

[Vividly]

Arcsec(0.1) =error
I/arccos(0.1)=.6799811946

What about? $$arcsec(\frac 1 x) = \frac{1} {\arccos x}$$Does that look better?

They both show up as errors. So what would make them show up as actual numbers?

 

[PeroK]

They both show up as errors. So what would make them show up as actual numbers?

They shouldn't have. Let's try to prove this anyway:

Let $z = arcsec(\frac 1 x)$, then $\sec z = \frac 1 x$, and $\cos z = \frac 1 {\sec z} = x$ and $z = \arccos x$.

So, it seems that we what really want is: $$\arccos x = arcsec(\frac 1 x)$$

 

[Vividly]

They shouldn't have. Let's try to prove this anyway:

Let $z = arcsec(\frac 1 x)$, then $\sec z = \frac 1 x$, and $\cos z = \frac 1 {\sec z} = x$ and $z = \arccos x$.

So, it seems that we what really want is: $$\arccos x = arcsec(\frac 1 x)$$

I guess what I am asking is how to find the derivative of y=1/arccos with a triangle. I am not sure how to put x=cos(1/y) on a right triangle to find the Hypotenuse, Opposite and Adjacent like I did for this problem.

 

[PeroK]

I guess what I am asking is how to find the derivative of y=1/arccos with a triangle. I am not sure how to put x=cos(1/y) on a right triangle to find the Hypotenuse, Opposite and Adjacent like I did for this problem.

An interesting idea. If you differentiate $y = \frac 1 {\arccos x}$, you must get an $\arccos^2 x$ term in the denominator. It's not going to come out as a polynomial in $x$.

 

[Vividly]

An interesting idea. If you differentiate $y = \frac 1 {\arccos x}$, you must get an $\arccos^2 x$ term in the denominator. It's not going to come out as a polynomial in $x$.

Yes, that's what I don’t understand how that came to be. The answer I get is 1/xsqrt(x^2-1). Did you do the quotient rule or did you do the power rule and bring arccos to the top then take the derivative?

 

[PeroK]

The answer I get is 1/xsqrt(x^2-1).

That can't be right. That's the derivative of $\arctan(\sqrt{x^2 - 1})$.

 

[jbriggs444]

I am confused about why you have all those number signs.

This sounds like you are seeing the LaTeX code rather than the resulting equations that are rendered. Refreshing the screen may help. Those do not always render properly -- though they showed up well for me.

Also, if you are responding to a post, the LaTeX code is helpfully presented in code form, rather than rendered form. This allows you to see how @PeroK composed the equations so that you can retrieve that quoted code and modify it to use in your response. See the LaTeX Guide below the editing window.

 

[Vividly]

That can't be right. That's the derivative of $\arctan(\sqrt{x^2 - 1})$.

Yes, I made a mistake because supposedly 1/arccosx ≠arcsec. I will try to write out my thoughts again and show you

 

[PeroK]

Yes, I made a mistake because supposedly 1/arccosx ≠arcsec.

There's no supposedly about it. They are definitely not the same thing.

 

[Vividly]

There's no supposedly about it. They are definitely not the same thing.

Well with that being said, I am trying to figure out how to make it into a triangle so I can know how to solve it from scratch without memorizing. Did you do the quotient rule or reciprocal rule to solve it? I am want to figure out how to get the polynomial under the square root.

 

[PeroK]

Well with that being said, I am trying to figure out how to make it into a triangle so I can know how to solve it from scratch without memorizing.

There's nothing to memorise to get inverse trig derivatives. You just use the chain rule: $$f^{-1}(f(x)) = x \ \Rightarrow \ (f^{-1})'(f(x))f'(x) = 1 \ \Rightarrow \ (f^{-1})'(f(x)) = \frac 1 {f'(x)}$$ For example:$$f(x) = \tan x \ \Rightarrow \ f'(x) = \sec^2 x = \tan^2 x + 1 \ \Rightarrow \ (\tan^{-1})'(\tan x) = \frac 1 {\tan^2 x + 1}$$$$\Rightarrow \ (\tan^{-1})'(x) = \frac 1 {x^2 + 1}$$

 

[Vividly]

There's nothing to memorise to get inverse trig derivatives. You just use the chain rule: $$f^{-1}(f(x)) = x \ \Rightarrow \ (f^{-1})'(f(x))f'(x) = 1 \ \Rightarrow \ (f^{-1})'(f(x)) = \frac 1 {f'(x)}$$ For example:$$f(x) = \tan x \ \Rightarrow \ f'(x) = \sec^2 x = \tan^2 x + 1 \ \Rightarrow \ (\tan^{-1})'(\tan x) = \frac 1 {\tan^2 x + 1}$$$$\Rightarrow \ (\tan^{-1})'(x) = \frac 1 {x^2 + 1}$$

I figured it out

 

[PeroK]

You have the wrong sign there. The derivative should be positive.

 

[Vividly]

You have the wrong sign there. The derivative should be positive.

Yes the negative on top and the one at the bottom cancel. I just didn’t show it canceling. Thank you for the help.

 

[Vividly]

They shouldn't have. Let's try to prove this anyway:

Let $z = arcsec(\frac 1 x)$, then $\sec z = \frac 1 x$, and $\cos z = \frac 1 {\sec z} = x$ and $z = \arccos x$.

So, it seems that we what really want is: $$\arccos x = arcsec(\frac 1 x)$$

What do you get when you put it in a calculator? I tried to resolve the problem but with arcsec(1/x) and got a different answer than the derivative of 1/arccosx

 

[anuttarasammyak]

Say
$$y=\frac{1}{\arccos x}$$
, calculation of its derivative is :
$$x=\cos\frac{1}{y}$$
$$dx=-\sin(\frac{1}{y})\ \ (-\frac{dy}{y^2})$$
$$\frac{dy}{dx}=\frac{y^2}{\sin\frac{1}{y}}=\frac{(\arccos x)^{-2}}{\sin(\arccos x)}=\frac{(\arccos x)^{-2}}{\pm\sqrt{1-x^2}}$$
arccos function is a multi-value function so we should be careful.

 

[PeroK]

What do you get when you put it in a calculator? I tried to resolve the problem but with arcsec(1/x) and got a different answer than the derivative of 1/arccosx

What calculation did you do?

 

[PeroK]

$$\frac{dy}{dx}=\frac{y^2}{\sin\frac{1}{y}}=\frac{(\arccos x)^{-2}}{\sin(\arccos x)}=\frac{(\arccos x)^{-2}}{\pm\sqrt{1-x^2}}$$
arccos function is a multi-value function so we should be careful.

For all $x \in [-1, 1]$ we have:$$\cos (\arccos x) = x$$$$\sin(\arccos x) = \sqrt{1-x^2}$$And, for $x \in [0, \pi]$$$\arccos(\cos x) = x$$But, for $x \in (\pi, 2\pi]$$$\arccos(\cos x) = 2\pi - x$$

 

[Vividly]

What calculation did you do?

Its completely different. Not sure what I am doing wrong. Unless arccos(x) ≠arcsec(1/x) like I stated at the top right of the board.

 

[PeroK]

Its completely different. Not sure what I am doing wrong. Unless arccos(x) ≠arcsec(1/x) like I stated at the top right of the board.

If you insist on your own idiosynchratic approach to trig identities, then I think the onus is on you to sort out the problems. I would encourage you to study this derivation. Let $x = \cos y$, with $y \in [0, \pi]$ :
$$\arccos(x) = \arccos(\cos y) = y$$ $$arcsec(\frac 1 x) = arcsec(\sec y) = y$$ QED

 

[Vividly]

Its completely different. Not sure what I am doing wrong. Unless arccos(x) ≠arcsec(1/x) like I stated at the top right of the board.

I think I know what I did wrong. I redid the problem and got the right answer. I just don’t understand how when you put values in the calculator for arccosx and arcsec(1/x) you get and error for one and a number for the other.

 

[PeroK]

I think I know what I did wrong. I redid the problem and got the right answer. I just don’t understand how when you put values in the calculator for arccosx and arcsec(1/x) you get and error for one and a number for the other.

The calculator on my phone doesn't have an option for $arcsec$; nor does excel (it seems); nor does $arcsec$ exist in Latex. None of that matters in light of post #31.

 

[Vividly]

The calculator on my phone doesn't have an option for $arcsec$; nor does excel (it seems); nor does $arcsec$ exist in Latex. None of that matters in light of post #31.

This youtube video teaches you how to put it in the calculator.

 

[PeroK]

I like that equation:$$\sec^{-1}(-2) = \cos^{-1}(-\frac 1 2) = \frac {2\pi}{3}$$