SUMMARY
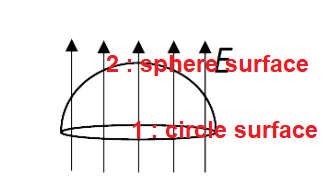
The discussion centers on the application of Gauss' Law to determine the electric flux through a half sphere and a flat surface. Participants confirm that the net electric flux is zero due to the absence of enclosed charge, leading to the conclusion that the flux through both surfaces is equal in magnitude but opposite in direction. The electric field is assumed to be homogeneous, allowing the use of Gauss' integral law for calculations. The conversation highlights the importance of defining normal directions when calculating electric flux through surfaces.
PREREQUISITES
- Understanding of Gauss' Law and its mathematical formulation.
- Familiarity with electric flux and its calculation through surfaces.
- Knowledge of the Divergence Theorem and its application in physics.
- Basic concepts of vector calculus, particularly surface integrals.
NEXT STEPS
- Study the Divergence Theorem and its implications in electromagnetism.
- Learn how to calculate electric flux using surface integrals in various geometries.
- Explore the relationship between electric field direction and flux sign conventions.
- Investigate the implications of using Gauss' Law in non-closed surfaces.
USEFUL FOR
Students and educators in physics, particularly those studying electromagnetism, as well as professionals seeking to deepen their understanding of electric fields and flux calculations.