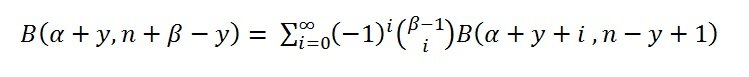chamilka said:
Hi everyone!
I got two versions of one particular function and now I need to show those two versions are equivalent.
For that I need to show the follwing,
View attachment 223
Is it possible to show this by using the properties of Beta functions, Gaussian hypergeometric function etc?
Thanks in advance!
Hi chamilka, :)
I got the intuition of solving this problem from your http://www.mathhelpboards.com/threads/1358-Chamilka-s-Question-from-Math-Help-Forum. Consider the integral, \(\displaystyle\int_{0}^{1}x^{y+\alpha-1}(1-x)^{(n+\beta-y)-1}\,dx\).
\begin{eqnarray}
\int_{0}^{1}x^{y+\alpha-1}(1-x)^{(n+\beta-y)-1}\,dx&=&\int_{0}^{1}x^{y+\alpha-1}(1-x)^{n-y}(1-x)^{\beta-1}\,dx\\
&=&\int_{0}^{1}x^{y+\alpha-1}(1-x)^{n-y}\sum_{i=0}^{\infty} \; {\beta-1\choose i}\;(-x)^{i}\,dx
\end{eqnarray}
Proceed with the same method I have gone through in http://www.mathhelpboards.com/threads/1358-Chamilka-s-Question-from-Math-Help-Forum?p=6487&viewfull=1#post6487, and you will finally get,
\[\int_{0}^{1}x^{y+\alpha-1}(1-x)^{(n+\beta-y)-1}\,dx=\sum_{i=0}^{\infty}(-1)^{i}{\beta-1\choose i}B(y+\alpha+i,\,n-y+1)~~~~~~~~~~~(1)\]
provided, \(Re(y+\alpha+i)>0\mbox{ and }Re(n-y+1)>0\).
Also by the definition of the
Beta function, if \(Re(y+\alpha)>0\mbox{ and }Re(n+\beta-y)>0\) we have,
\[\int_{0}^{1}x^{y+\alpha-1}(1-x)^{(n+\beta-y)-1}\,dx=B(y+\alpha,\,n+\beta-y)~~~~~~~(2)\]
From (1) and (2) we get,
\[B(y+\alpha,\,n+\beta-y)=\sum_{i=0}^{\infty}(-1)^{i}{\beta-1\choose i}B(y+\alpha+i,\,n-y+1)\]
provided, \(Re(y+\alpha)>0,\,Re(n-y+1)>0\mbox{ and }Re(n+\beta-y)>0\)
Kind Regards,
Sudharaka.