Why is this volume/surface integration unaffected by a singularity?

[Mike400]

$\mathbf{M'}$ is a vector field in volume $V'$ and $P$ be any point on the surface of $V'$ with position vector $\mathbf {r}$

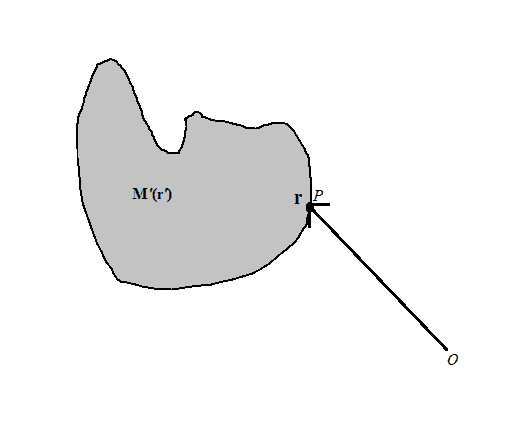
Now by Gauss divergence theorem:

\begin{align}
\iiint_{V'} \left[ \nabla' . \left( \dfrac{\mathbf{M'}}{\left| \mathbf{r}-\mathbf{r'} \right|} \right) \right] dV'
&=\unicode{x222F}_{S'} \left[ \left( \dfrac{\mathbf{M'}}{\left| \mathbf{r}-\mathbf{r'} \right|} \right) . \hat{n} \right] dS' \tag{1}\\
\end{align}

Both of these expressions, $LHS$ and $RHS$ of equation $(1)$, have their respective integrands singular at $\mathbf{r'}=\mathbf{r}$. Now how shall we show that both the volume and surface integration is unaffected by this singularity at $\mathbf{r'}=\mathbf{r}$?

 

[andrewkirk]

The expression above is not valid, because the divergence theorem is only applicable to continuously differentiable vector fields, and the vector field
$$
\dfrac{\mathbf{M'}}{\left| \mathbf{r}-\mathbf{r'} \right|}$$
is discontinuous at $\mathbf r$.

 

[Mike400]

Using the vector identity $\nabla.(\psi \mathbf{A})=\mathbf{A}.(\nabla \psi)+\psi (\nabla.\mathbf{A})$, $LHS$ of equation $1$ can be written as:

\begin{align}
\iiint_{V'} \left[ \nabla' . \left( \dfrac{\mathbf{M'}}{\left| \mathbf{r}-\mathbf{r'} \right|} \right) \right] dV'
&=\iiint_{V'} \mathbf{M'}.\nabla' \left( \dfrac{1}{\left| \mathbf{r}-\mathbf{r'} \right|} \right) dV'
+
\iiint_{V'} \dfrac{\nabla' . \mathbf{M'}}{\left| \mathbf{r}-\mathbf{r'} \right|} dV'
\tag{2}
\end{align}

Now for simplicity, let's take the origin of our coordinate system at $P$ (see the diagram). Thus equation $(2)$ becomes:

\begin{align}
\iiint_{V'} \left[ \nabla' . \left( \dfrac{\mathbf{M'}}{r'} \right) \right] dV'
&=\iiint_{V'} \mathbf{M'}.\nabla' \left( \dfrac{1}{r'} \right) dV' \tag{3}
&+\iiint_{V'} \dfrac{\nabla' . \mathbf{M'}}{r'} dV'\\
\end{align}

Now by writing $dV'$ as spherical volume element, equation $(3)$ becomes:

$\displaystyle \iiint_{V'} \left[ \nabla' . \left( \dfrac{\mathbf{M'}}{r'} \right) \right] {r'}^2\ \sin\theta\ d\theta\ d\phi\ dr' =\iiint_{V'} \mathbf{M'}.\nabla' \left( \dfrac{1}{r'} \right) {r'}^2\ \sin\theta\ d\theta\ d\phi\ dr' +\iiint_{V'} \dfrac{\nabla' . \mathbf{M'}}{r'} {r'}^2\ \sin\theta\ d\theta\ d\phi\ dr'\\ \displaystyle =\iiint_{V'} (\mathbf{M'}. \hat{r'}) \sin\theta\ d\theta\ d\phi\ dr' +\iiint_{V'} (\nabla' . \mathbf{M'})\ r'\ \sin\theta\ d\theta\ d\phi\ dr'\\ \tag{4}$

In equation $(4)$, the integrands are defined everywhere except at $P$ where $r'=0$ where the integrand is $\frac{0}{0}$. Thus we can directly compute the volume integrals in equation $(4)$. Can we now do something to apply the Gauss divergence theorem to the $LHS$ of equation $(4)$?