Is Moment of Inertia Dependent on Surface Movement Away from Axis?

[Guillem_dlc]

Homework Statement

Find the angle of the principal axes where $x'$ and $y'$ are the principal axes.

Relevant Equations

Last figure of the solution

Statement figure:

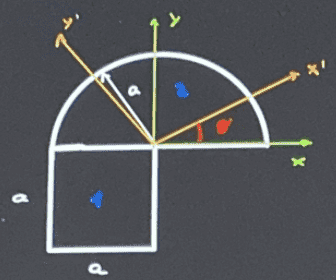
My attempt at a solution:
FIGURE 1 $\rightarrow A=a^2$

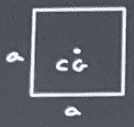
CG $\rightarrow \overline{x}=-a/2, y=-a/2$
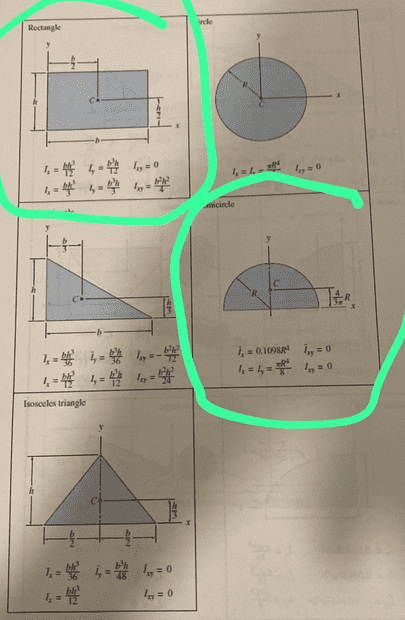
$$\overline{Ix}_1=\dfrac{bh^3}{12}=\overline{Iy}_1=\dfrac{a^4}{12}$$
$$Ix_1=\overline{Ix}_1+\overline{y}^2A=\dfrac{a^4}{12}+\dfrac{a^4}{4}=\dfrac13 a^4\, \textrm{mm}^4=Iy_1$$
$$\overline{Ixy}_1=0\, \textrm{mm}^4\rightarrow Ixy_1=\dfrac{a^4}{4}$$

FIGURE 2 $\rightarrow A=\dfrac{\pi a^2}{2}$

CG $\rightarrow \overline{x}=0, \overline{y}=\dfrac{4\pi}3a$
$$Ix_2=Iy_2=\dfrac{\pi}8a^4\, \textrm{mm}^4,\,\, \overline{Ixy}=0\rightarrow Ixy=0+0\cdot \overline{y}A=0\, \textrm{mm}^4$$
$$Ix=\sum Ix_i=0,76032a^4\, \textrm{mm}^4$$
$$Iy=\sum Iy_i=0,76032a^4 \, \textrm{mm}^4$$
$$Ixy=\sum Ixy_i=\dfrac 14a^2$$
$$\boxed{\sigma =\dfrac12 \arctan \left( \dfrac{-2Ixy}{Ix-Iy}\right)=\dfrac12 \arctan (-\infty)=-45^\circ}$$

If you could tell me if it's ok you would do me a big favor. thank you very much!

The moment of inertia depended on how the surface moves away from the axis, right? Because if so maybe it does make sense that I got the two equal moments ($x$ and $y$), doesn't it?

 

[TSny]

Your work for obtaining $I_x$ and $I_y$ looks correct. However, when I calculate $\pi/8 + 1/3$, I get 0.726 instead of 0.760. But, the important thing for this problem is that $I_x = I_y$. Many books use the notation $I_{xx}$ and $I_{yy}$ for your $I_x$ and $I_y$. Also, many books define $I_{xy}$ to have the opposite sign of your definition. But, I've seen both definitions used.

The question asks for the angles of orientation of the principal $x'$ and $y'$ axes. You calculated one angle equal to -45^o. So, I think you should include some comments regarding how this calculated angle relates to the orientation of the $x'$ and $y'$ axes.

The moment of inertia depended on how the surface moves away from the axis, right? Because if so maybe it does make sense that I got the two equal moments ($x$ and $y$), doesn't it?

Yes, if you study how the mass is distributed about the $x$ and $y$ axes for this problem, then I think you can see that $I_{xx}$ should equal $I_{yy}$ without doing any calculation.

 

[Guillem_dlc]

Your work for obtaining $I_x$ and $I_y$ looks correct. However, when I calculate $\pi/8 + 1/3$, I get 0.726 instead of 0.760. But, the important thing for this problem is that $I_x = I_y$. Many books use the notation $I_{xx}$ and $I_{yy}$ for your $I_x$ and $I_y$. Also, many books define $I_{xy}$ to have the opposite sign of your definition. But, I've seen both definitions used.

The question asks for the angles of orientation of the principal $x'$ and $y'$ axes. You calculated one angle equal to -45^o. So, I think you should include some comments regarding how this calculated angle relates to the orientation of the $x'$ and $y'$ axes.
Yes, if you study how the mass is distributed about the $x$ and $y$ axes for this problem, then I think you can see that $I_{xx}$ should equal $I_{yy}$ without doing any calculation.

$0,726$ yes sorry I left out the $2$.

That would be fine then, wouldn't it?

 

[TSny]

$0,726$ yes sorry I left out the $2$.

That would be fine then, wouldn't it?

Yes. Hopefully, the orientations of the principal axes are clear to you from your answer for the angle $\sigma$.

 

[Guillem_dlc]

Yes. Hopefully, the orientations of the principal axes are clear to you from your answer for the angle $\sigma$.

I was told that the $x$-axis was going to be the minimum and with $-45$ I was left with the maximum.

So I put that changing the angle to $45$ would leave the $x$ as the minimum.

 

[TSny]

I was told that the $x$-axis was going to be the minimum and with $-45$ I was left with the maximum.

So I put that changing the angle to $45$ would leave the $x$ as the minimum.

I don't understand what it means to say that the $x$-axis is a minimum or a maximum. The important thing is to be able to draw or describe the orientation of the principal axes.

 

[Guillem_dlc]

I don't understand what it means to say that the $x$-axis is a minimum or a maximum. The important thing is to be able to draw or describe the orientation of the principal axes.

Apart from finding this principal angle, it was requested that the $x'$ axis (that is, the $x$-axis of the principal axis) should be the minimum and the $y$-axis the maximum. That is to say, about the principal axes, that there is one that must have a maximum moment of inertia and another one a minimum. So they told you that the principal $x$-axis of inertia should be the minimum. So if you looked at the moment of inertia of each axis with the angle of $-45^\circ$, then you got that the $x$ is the maximum and the $y$ is the minimum. And then I thought about the angle of $45^\circ$, which in the end is the same. And then the moment of inertia of $x$ was already the minimum, you know?

 

[TSny]

OK. I see now. I agree that the principal moment of inertial about the axis at +45^o would be smaller than the principal moment of inertia about the axis at -45^o.

 

[Guillem_dlc]

OK. I see now. I agree that the principal moment of inertial about the axis at +45^o would be smaller than the principal moment of inertia about the axis at -45^o.

Okay, so it would be fine then, wouldn't it?

 

[TSny]

I believe so.