Moment of Inertia of Hollow Sphere about Center Axis x-y-z method

[howie8594]

Homework Statement

Find the moment of inertia of a hollow sphere about a vertical axis through its center in terms of its mass M and radius R.

Homework Equations

I=\int r^{2} dm

The Attempt at a Solution

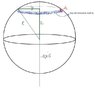
I've been curious about different methods for finding moments of inertia. I've only seen the moment of inertia of a hollow sphere found by taking tiny rings touching the inner edge of the sphere and taking an infinite number of them extending from the top of the sphere to the bottom of the sphere. That was done by taking the horizontal component of the radius of the sphere Rcosθ and integrating from -\pi/2 to \pi/2 with respect to θ. I tried it that way and got 2/3MR^2, which is the right answer. What I don't understand is why integrating with respect to the z-axis wouldn't work also. I've tried it several times and have not gotten the right answer. I've attached a picture that attempts to explain my thinking on that a little. Anyway, here's what I did:


The moment of inertia of a ring is mr^{2}. So a small ring making up a small part of the sphere would have a moment of inertia:

dI=r^{2}dm=y^{2}dm. (y is the radius of any ring in the sphere).

The mass M of the sphere would be:

M=σA, where σ is the surface density measured in kg/m^2 and A is the total surface area of the sphere. I used surface density instead of regular volume density because the hollow sphere shouldn't have any thickness in the x or y direction theoretically; so as far as the mass is concerned, the sphere only has 2 dimensions. Written as a differential,

dm=σda. → σ=\dfrac{M}{A}=\dfrac{M}{4πR^{2}} → dm=\dfrac{M}{4πR^{2}}da=\dfrac{M}{4πR^{2}}*2πydz=\dfrac{My}{2R^{2}}dz.

(y is the radius of any ring in the sphere and 2πy is the circumference of that ring. So 2πy dz is that circumference times a small depth along the z-axis. That equals the small area element da). Now,

dI=y^{2}\dfrac{My}{2R^{2}}dz=y^{3}\dfrac{M}{2R^{2}}dz.

Looking at the attached diagram, it's easy to see that using Pythagorean's Theorem,

y^{2}=R^{2}-z^{2}. I substituted this back into the original differential and got:

dI=(R^{2}-z^{2})^{3/2}\dfrac{M}{2R^{2}}dz.

Integrating both sides,

I=\dfrac{M}{2R^{2}}\int(R^{2}-z^{2})^{3/2}dz.

To sum an infinite number of rings from the bottom of the sphere to the top of the sphere, I integrated from -R to R.

I=\dfrac{M}{2R^{2}}\int^{R}_{-R}(R^{2}-z^{2})^{3/2}dz.

Now, this looked to me like a pain to evaluate, but I ran it through a calculator and got:

I=\dfrac{M}{2R^{2}}\int^{R}_{-R}(R^{2}-z^{2})^{3/2}dz=\dfrac{M}{2R^{2}}*\dfrac{3πR^{4}}{8}

=\dfrac{3}{16}πMR^{2}.

This is obviously wrong, but I see no reason why this method wouldn't work. Where did I go wrong?

Thanks everyone!

 

[ehild]

M=σA, where σ is the surface density measured in kg/m^2 and A is the total surface area of the sphere. I used surface density instead of regular volume density because the hollow sphere shouldn't have any thickness in the x or y direction theoretically; so as far as the mass is concerned, the sphere only has 2 dimensions. Written as a differential,

dm=σda. → σ=\dfrac{M}{A}=\dfrac{M}{4πR^{2}} → dm=\dfrac{M}{4πR^{2}}da=\dfrac{M}{4πR^{2}}*2πydz=\dfrac{My}{2R^{2}}dz.

(y is the radius of any ring in the sphere and 2πy is the circumference of that ring. So 2πy dz is that circumference times a small depth along the z-axis. That equals the small area element da).

No, the area element is equl to the circumference times the thickness of the "ribbon", that is da=2\pi y ds =2\pi y \sqrt{(dy)^2+(dz)^2}=2\pi y \sqrt{1+(\frac{dy}{dz})^2}dz
ehild

 

[howie8594]

Oh ok that makes sense. I got the right answer doing it that way. Now I see why everyone uses the angle method instead. Thanks ehild.

 

[ehild]

You are welcome.

ehild