- 1,864
- 34
I have written a proof of the simons line theorem. I would appreciate if someone would tell me if it's complete.
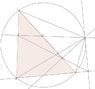
We have \Delta ABC inscrubed in a circle, and P is an arbitrary point that does not coincide with either of the corners of the triangle. (See attached figure).
Now draw perpendiculars from P to [AB], [AC] and [BC] which intersect with the lines in U, \ Y and Z respectively.
Let E be the point of intersection between [PU] and [AY].
Let T be the point of intersection between [AC] and [BP].
Let \angle BZP=\alpha and \angle APU=\beta.
Now as \angle BZP and \angle BUP are supplementary, BZPU is a cyclic quadrilateral \Rightarrow \angle PUZ = \alpha.
Now as \angle PAC subtend over the same arc as \angle PBZ, \ \angle PAC = \alpha \Rightarrow \angle UAR = 90 - (\alpha +\beta) \Rightarrow \angle ARU = \alpha + \beta \Rightarrow \angle PET = \alpha +\beta.
Let \angle UZB = \gamma \Rightarrow \angle UPB = \gamma.
As \angle CYP and \angle CZP are supplementary, CZPY is a cyclic quadrilateral \Rightarrow \angle CPY = \gamma.
As \angle PAY =\angle PUY, APYU is a cyclic quadrilateral \Rightarrow \angle UYA = \beta.
Now \angle ETP =180-(\alpha +\beta + \gamma) \Rightarrow \angle PTY = \alpha +\beta +\gamma \Rightarrow \angle TPY=90-(\alpha+\beta+\gamma)
Now as \angle BUZ=\angle BPZ and \angle BUZ=90 - \alpha, \angle BPZ = 90 - \alpha.
Let \angle CPZ= \mu. Now \angle CPZ+\angle TPC=\angle BUZ \Rightarrow \mu + 90-(\alpha +\beta)=90-\alpha \Rightarrow \mu = \beta \Rightarrow \angle CPZ = \beta \Rightarrow CYZ = \beta.
As \angle UYP+\angle PYZ = \beta +90 + 90-\beta = 180, U, \ Y and Z must be colinear.
QED
Thanks for any feedback.
We have \Delta ABC inscrubed in a circle, and P is an arbitrary point that does not coincide with either of the corners of the triangle. (See attached figure).
Now draw perpendiculars from P to [AB], [AC] and [BC] which intersect with the lines in U, \ Y and Z respectively.
Let E be the point of intersection between [PU] and [AY].
Let T be the point of intersection between [AC] and [BP].
Let \angle BZP=\alpha and \angle APU=\beta.
Now as \angle BZP and \angle BUP are supplementary, BZPU is a cyclic quadrilateral \Rightarrow \angle PUZ = \alpha.
Now as \angle PAC subtend over the same arc as \angle PBZ, \ \angle PAC = \alpha \Rightarrow \angle UAR = 90 - (\alpha +\beta) \Rightarrow \angle ARU = \alpha + \beta \Rightarrow \angle PET = \alpha +\beta.
Let \angle UZB = \gamma \Rightarrow \angle UPB = \gamma.
As \angle CYP and \angle CZP are supplementary, CZPY is a cyclic quadrilateral \Rightarrow \angle CPY = \gamma.
As \angle PAY =\angle PUY, APYU is a cyclic quadrilateral \Rightarrow \angle UYA = \beta.
Now \angle ETP =180-(\alpha +\beta + \gamma) \Rightarrow \angle PTY = \alpha +\beta +\gamma \Rightarrow \angle TPY=90-(\alpha+\beta+\gamma)
Now as \angle BUZ=\angle BPZ and \angle BUZ=90 - \alpha, \angle BPZ = 90 - \alpha.
Let \angle CPZ= \mu. Now \angle CPZ+\angle TPC=\angle BUZ \Rightarrow \mu + 90-(\alpha +\beta)=90-\alpha \Rightarrow \mu = \beta \Rightarrow \angle CPZ = \beta \Rightarrow CYZ = \beta.
As \angle UYP+\angle PYZ = \beta +90 + 90-\beta = 180, U, \ Y and Z must be colinear.
QED
Thanks for any feedback.
Attachments
Last edited: