davidge
- 553
- 21
I was interested in finding a motivation for the generalized Stokes' theorem. I was asking myself why
$$ \int_D d \omega = \int_{\partial D} \omega $$ for a region ##D## and a (p-1)-dimensional form ##\omega##.
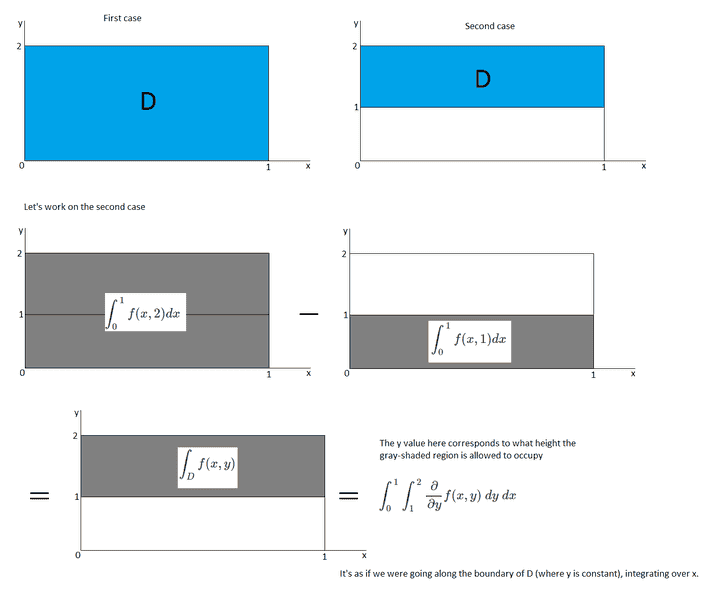
Then I found something funny when working with some arbitrary functions in two dimensions. Below is what I found.
In the second image, I called ##x^{\mu}_{i}## and ##x^{\mu}_{f}## the coordinates of the initial and final points, respectively.
My question is: Is this actually correct?

$$ \int_D d \omega = \int_{\partial D} \omega $$ for a region ##D## and a (p-1)-dimensional form ##\omega##.
Then I found something funny when working with some arbitrary functions in two dimensions. Below is what I found.
In the second image, I called ##x^{\mu}_{i}## and ##x^{\mu}_{f}## the coordinates of the initial and final points, respectively.
My question is: Is this actually correct?