FrankJ777
- 140
- 6
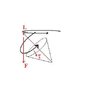
I'm curious about how precession works. From what I thought I understood about angular momentum and torque vectors, the direction that they point are by arbitrary convention using the right hand rule. They are just a convenient expression of the normal or the plane that the torque acts on the moment arm and the magnitude, or in the case of angular momentum, the vector describes the magnitude and the normal of the plane the mass is rotating in. The way I understand precession is that a force acts on the angular momentum vector, which produces a torque with a vector pointing from the normal of the plane that the force vector and angular momentum vector produce.
What's odd to me though, is that I thought the angular momentum vector and torque vector directions were an arbitrary convention, but they seem to act like ordinary force vectors and moment arms, in that the force F acts on L as though it were a moment arm and produces the torque vector, \tau which seems to act like a conventional force vector, causing L to have an angular acceleration. I don't understand how it works if the direction of L and \tau are just arbitrary conventions. It seems like there is something more I'm missing. could someone please clear it up for me. Thanks
What's odd to me though, is that I thought the angular momentum vector and torque vector directions were an arbitrary convention, but they seem to act like ordinary force vectors and moment arms, in that the force F acts on L as though it were a moment arm and produces the torque vector, \tau which seems to act like a conventional force vector, causing L to have an angular acceleration. I don't understand how it works if the direction of L and \tau are just arbitrary conventions. It seems like there is something more I'm missing. could someone please clear it up for me. Thanks