Is Snell's law incompatible with interface conditions? What went wrong?

[Ngineer]

Hi everyone,

Someone posted this hypothetical problem on a facebook group and I am wondering what your thoughts are.

The issue is that Snell's law does not seem to hold when applied to the transmitted wave (calculated using the electromagnetic interface conditions.) Here is an example:

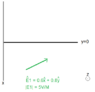
Suppose we have an interface at y=0 between vacuum (medium 1; n1 = 1) and a material of εr = μr = 10 (medium 2; n2 = 10).

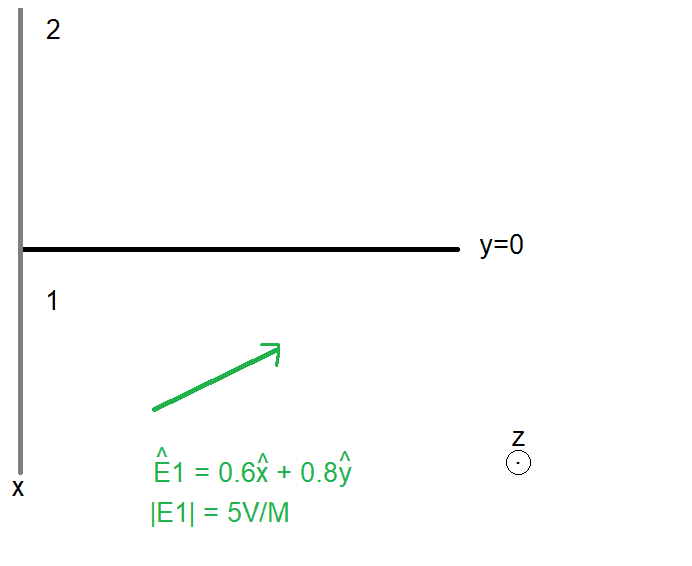
For a plane electromagnetic wave whose electric field is given by the green arrow, we subsequently have:

And a propagation direction along E1xH1:

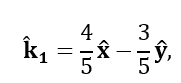
which corresponds to an angle of 36.87 degrees.

Using the interface conditions, we find that in the second medium, E2 has a unit vector of (x+ 0.132y), and that H2 is in a direction identical to H1 (i.e. z).
This gives rise to a propagation direction of
k2 = -0.132x + y

Which corresponds to an angle of 82.47 degrees.

Now the problematic issue is:
sin(theta2) / sin(theta1) = sin(82.47)/sin(36.87) = 1.65
Whereas
n1/n2 = 1/10 = 0.1.

Doesn't Snell's law stipulate that they're equal? What went wrong?

 

[Andy Resnick]

I don't understand how you determined E2 and H2: "Using the interface conditions, we find that in the second medium, E2 has a unit vector of (x+ 0.132y), and that H2 is in a direction identical to H1 (i.e. z). "

 

[Ngineer]

Hi Andy,
E1 = 5V/M * [0.6,0.8] = [3,4,0] V/M
Using the conditions for continuity at the interface:
E2x = E1y = 3
E2y = E1y * (epsilon1/epsilon2) = 4 * 1/10 = 0.4
So E2 = [3, 0.4, 0] V/M
= 3.02 V/M * [ 0.991, 0.1321, 0 ]
For H2,
H1 = [0,0,5/377] A/M Hence H2z = H1z * meu1/meu2 = 0.5/377 A/M

(This got me even wondering, how does the continuity stipulate that H1z = H2z = 5/377 A/M, when due to propagation we require H2z = 3.02/377 A/M!)

 

[Andy Resnick]

One error: n = √(ε_r μ_r), so if n = 10 and μ_r = 1 (valid for dielectrics), then ε_r = 100.

 

[Ngineer]

One error: n = √(ε_r μ_r), so if n = 10 and μ_r = 1 (valid for dielectrics), then ε_r = 100.

For the second medium, εr = μr = 10

 

[ZapperZ]

The claim of this thread is very odd, considering that one of things that a student in an E&M course often do is to DERIVE Snell's law using Maxwell equations and the boundary conditions, such as this:

https://ocw.mit.edu/courses/materia...-2013/lecture-notes/MIT3_024S13_2012lec22.pdf
Zz.

 

[Ngineer]

The claim of this thread is very odd, considering that one of things that a student in an E&M course often do is to DERIVE Snell's law using Maxwell equations and the boundary conditions, such as this:

https://ocw.mit.edu/courses/materia...-2013/lecture-notes/MIT3_024S13_2012lec22.pdf
Zz.

I'm not making a claim, I'm asking what went wrong in this particular derivation because I can't figure it out.

 

[DrDu]

Did you consider the reflected wave?

 

[Ngineer]

Did you consider the reflected wave?

Thanks! that was probably it!