Is the change in internal energy really a state function?

[msw1]

Homework Statement

(Figure 1) shows two processes, A and B, for moving 3.45 × 10^22 particles of a monatomic ideal gas from state i to state f. Which process requires a smaller magnitude of the energy Q transferred thermally to the gas?

Relevant Equations

$$\Delta E=W+Q$$
$$PV=Nk_BT$$
$$Q=\tfrac{d}{2}Nk_BT \text{ (isochoric process)}$$
$$Q=NC_p\Delta T \text{ (isobaric process) }$$

Here is the figure:

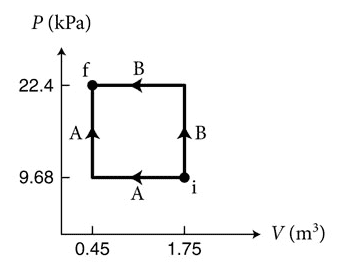
The answer is $$Q_A<Q_B$$ which I can show by calculation using the above equations. What's confusing to me is I thought that the change in internal energy was a state function. Which would mean since the initial and final points are the same, $$\Delta E_A=\Delta E_B$$ or by the 1st law of thermodynamics $$W_A+Q_A=W_B+Q_B$$ Since W is the area under the curve (and positive in this case since the gas is being compressed), $$W_A<W_B$$ So the work done on the gas in process A is less than in process B, and the energy transferred thermally to the gas in process A is less than in process B. Which, since all values are positive, seems like it contradicts the original assumption that the change in internal energy was a state function, since it seems like the change in internal energy has to be less in process A. What am I missing here?

 

[mfb]

The answer is $Q_A<Q_B$ which I can show by calculation using the above equations.

Can you show that calculation? There is heat involved in both parts of both transitions.

 

[msw1]

Can you show that calculation? There is heat involved in both parts of both transitions.

Sure, energy transferred thermally in the isobaric processes is
$$Q=NC_p\Delta T$$
$$Q=N\left(\tfrac{d}{2}+1\right)k_b\Delta T$$
And $\Delta T = \frac{P\Delta V}{Nk_B}$ by the ideal gas law so
$$Q=P\Delta V\left(\tfrac{d}{2}+1\right)$$
And then for the isochoric processes
$$Q=\tfrac{d}{2}Nk_B\Delta T$$
And $\Delta T = \frac{\Delta P V}{Nk_B}$ so
$$Q = \tfrac{d}{2}(\Delta P)V$$
So the overall energy transferred thermally in each process is
$$P\Delta V\left(\tfrac{d}{2}+1\right)+\tfrac{d}{2}(\Delta P)V$$
Taking d to be 3 since this is a monatomic gas, the energy transferred thermally in process A is then
$$9680\cdot1.3(\tfrac{3}{2}+1)+\tfrac{3}{2}\cdot12720\cdot0.45=40046J$$
And then the energy transferred thermally in process B is
$$22400\cdot1.3(\tfrac{3}{2}+1)+\tfrac{3}{2}\cdot12720\cdot1.75=106190J$$
So $Q_A<Q_B$, which my homework grader says is correct.

 

[mfb]

What is the sign of $\Delta V$?

 

[msw1]

What is the sign of $\Delta V$?

Oh, that was it! So $|Q_A|<|Q_B|$ like the question asked, but $Q_A>Q_B$, and so there is no contradiction. Thanks!