mathmari
Gold Member
MHB
- 4,984
- 7
Hello! 
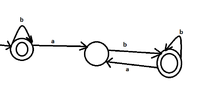
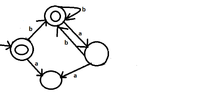
I have to construct the DFA of the language $L=\{w \in \{a,b\}^*: \text{ each } "a" \text{ of the word w is appeared only after and before a } "b"\}$.
I tried the following...Could you tell if it's right?
But is it deterministic? From the second state where do we go with $a$ ?
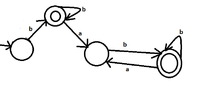
I have to construct the DFA of the language $L=\{w \in \{a,b\}^*: \text{ each } "a" \text{ of the word w is appeared only after and before a } "b"\}$.
I tried the following...Could you tell if it's right?
But is it deterministic? From the second state where do we go with $a$ ?
Attachments
Last edited by a moderator: