Is There a Missing Load in My Statically Indeterminate Shaft Calculation?

[yonese]

Homework Statement

I'm trying to solve for this intederminate beam for an output shaft for a gearbox I'm designing. I have 3 bearings (1 deep groove, 1 needle and 1 cylindrical) and I have assumed that axial load is negligible.

Relevant Equations

P = A+B+C

I have drawn the bending moment diagram to try to help me determine the moment, but I am certain my values are wrong. I have included a picture of my gearbox design, where the bottom shaft is what I'm trying to calculate. I've been able to calculate the top shaft moments and reaction forces with no problem. (Bending moment = 30.63 Nm, ball bearing = 850.8 N, roller bearing = 928.2N, Torque = 55.2 Nm)

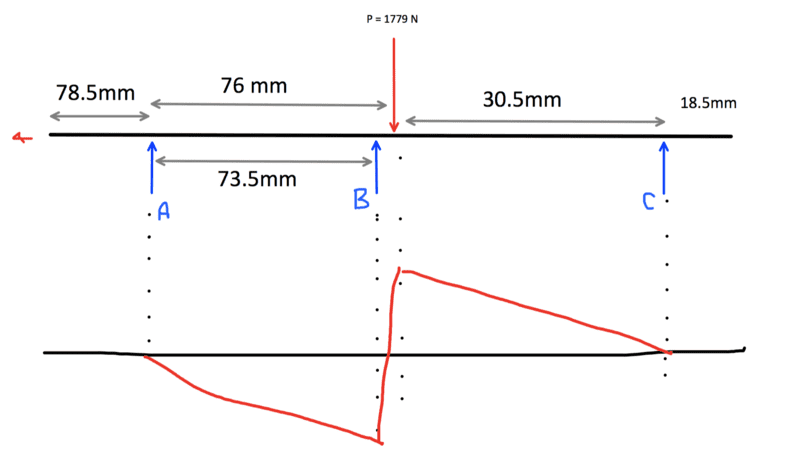
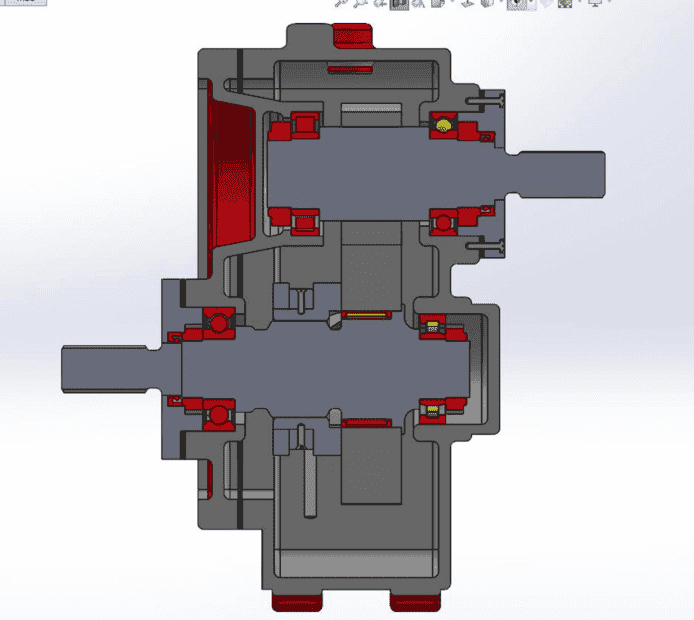
For the bottom shaft, I am given that the torque is 107.8 Nm and I managed to get moment = 2.98 Nm, which just doesn't seem likely. My calculated reaction forces for the bearings are
Ball = 17 N
Needle = 1700 N
Roller = 98 N

It doesn't seem likely that the needle bearing would take so much of the load, considering the magnitude of my previous answers.

Is there a second load that I am missing? Or prehaps I should be taking the shaft and gear as a UDL?

 

[PhanthomJay]

I'm not into gears and such, but your load diagram shows the concentrated load of 1779 N practically right on top of the needle support B, implying B will take most all of the up reaction load, with small down reaction at A, and small up reaction at C, and there will be very little bending moment in the shaft, so your analysis is correct for the loading shown. But whether your load model is correct is another story.

 

[Dr.D]

Are you familiar with the "unit load" method? If so, that will resolve this problem rather quickly.