Is there a way to calculate this transformation?

[wirefree]

Namaste & G'day!

Imagine a helicopter view of a Polo ground. It's length & breadth are known.

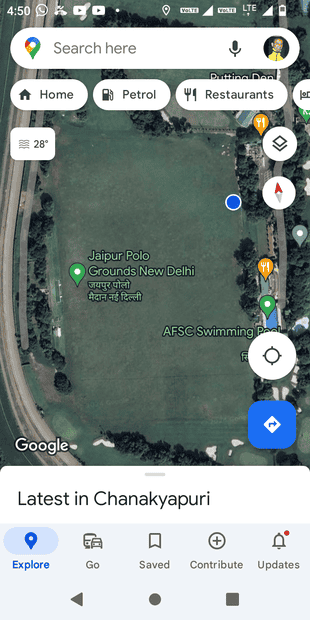
Now you are seated where the blue dot is. Your view is such:

How do mathematicians calculate the distance travelled by a ball from the second perspective?

From the top view, this would be trivial.

But now your view is transformed.

 

[Frabjous]

I think of the second prespective in cylindrical coordinates (r,θ). θ is “easy” to determine, r is more difficult. In a perfect world, one could measure the diameter of the ball to determine its distance. There are other experimental techniques, but I am unsure exactly what you are looking for.

 

[FactChecker]

Suppose the eye-point location is at the center of the polar coordinates ($r_{eye}=0$) and the angle, $\theta$, of the polar coordinates of the ball are known. The distance to the ball location, $r$, remains to be determined. Assuming a flat earth, $r$ can be calculated using trigonometry. You would need to know the distance to the tree-line. That tree-line has sides and its distance would require some calculations that depend on the direction.

 

[wirefree]

I think of the second prespective in cylindrical coordinates (r,θ). θ is “easy” to determine, r is more difficult. In a perfect world, one could measure the diameter of the ball to determine its distance. There are other experimental techniques, but I am unsure exactly what you are looking for.

Here's a view:

You see how the perspective view squashes the 160yd width of the polo field.

 

[wirefree]

Suppose the eye-point location is at the center of the polar coordinates ($r_{eye}=0$) and the angle, $\theta$, of the polar coordinates of the ball are known. The distance to the ball location, $r$, remains to be determined. Assuming a flat earth, $r$ can be calculated using trigonometry. You would need to know the distance to the tree-line. That tree-line has sides and its distance would require some calculations that depend on the direction.

I am interested in following your suggestion. Please annotate as briefly as convenient, Sir.