Is there an analytic solution to this system of equations?

[END]

I have the following system of equations with variables $a,m$, and I'm wondering—can this system be solved symbolically/analytically?

\begin{align}
m &= 100 + \frac{ \left( 200 \frac{\ln{\frac{1}{2}}}{26.8} \right) }{\left(\dfrac{\ln{\frac{1}{2}}}{26.8} + a \right)}
\\ \\
50 &= me^{-a\left( 19.9 \right)}- \frac{ \left( 200 \frac{\ln{\frac{1}{2}}}{26.8} \right) \exp{ \left(\dfrac{\ln{\frac{1}{2}}}{26.8} \cdot 19.9 \right) }}{\left(\dfrac{\ln{\frac{1}{2}}}{26.8} + a \right)}
\end{align}

(What are some ways to recognize that a problem does or does not have an analytic solution?)

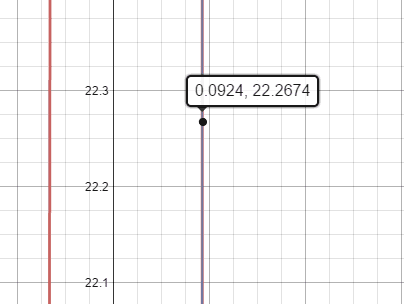
For this specific example, I understand the answers can be numerically approximated to

\begin{align}
a &\approx 0.092409
\\
m &\approx 22.2674
\end{align}

Via such numerical methods as a graph:

or other computational device such as WolframAlpha [(link to this problem). For this specific problem, WolframAlpha only provided a numerical approximation.

Note: The variables in the WolframAlpha link are $a, n$ respectively

 

[jedishrfu]

If you replace the factor ln(0.5)/26.8 with K and use x and y for a and m you get for the first equation:

y = 100 + 200K/(x+K)

and for the second you get:

50/e^19.9 = y - 200Ke^K/(x+K)

which rearranges to:

y = 50/e^19.9 + 200e^K/(x+K)

From here you can set the equations equal to each other and solve for x noting that x=/= -K

 

[TheoMcCloskey]

I don't see an analytical solution. For a numerical solution, consider the following:

With
\begin{align*}
m &= 100 + 200 \cdot \frac{\beta}{\beta+a} \\
50 &= m \cdot e^{-19.9a} - 200 \cdot \frac{\beta}{\beta+a} \cdot e^{19.9 \cdot \beta}
\end{align*}
Where \beta = \ln(1/2) / 26.8 \approx -0.02586.

Multiply the second equation by \exp{(19.9 \cdot a)}
\begin{equation*}
50 \cdot e^{19.9 \cdot a} = m - 200 \cdot \frac{\beta}{\beta + a} \cdot e^{19.9 \cdot \beta} \cdot e^{19.9 \cdot a}
\end{equation*}

Let w= \beta + a and substitute first equation into second to yield
\begin{equation*}
c \cdot e^{19.9 \cdot w} = \left[100 + 200 \cdot \frac{\beta}{w}\right] - 200 \cdot \frac{\beta}{w} \cdot e^{19.9 \cdot w}
\end{equation*}
where c = 50 \cdot e^{-19.9 \cdot \beta} \approx 83.6558.

This is a non-linear scalar equation in one parameter w. A numerical solution will be necessary. Before we go down that path, re-scale and introduce a non-parametric variable for w. Let \alpha = a / \beta, \zeta = w / \beta = 1 + \alpha and re-formulate into F(\zeta) = 0.

\begin{equation*}
F(\zeta) = 0 = 100 \cdot \left[ \left(\gamma + \frac{2}{\zeta}\right) \cdot e^{\lambda \cdot \zeta} - \left(1 + \frac{2}{\zeta}\right) \right]
\end{equation*}
where \gamma = c / 100 and \lambda = 19.9 \cdot \beta \approx -.51469.

This could be solved numerically, but we don't know the magnitude or an applicable domain bracket that contains a (ie, \zeta). If we look at the above equation for F, we see it is equivalent to
\begin{equation*}
F(\zeta) = 100 \cdot \left[
\left(1 + \frac{2}{\zeta}\right) \cdot \left(e^{\lambda \cdot \zeta} -1\right) - \mu \cdot e^{\lambda \cdot \zeta}\right]
\end{equation*}
where \mu = 1 - \gamma \approx .167.

If we ignored the last term, we would underestimate F (since \mu > 0 and the exponential is positive). But if we did, we would see that two conditions could result in F= 0:

First: \exp{(\lambda \cdot \zeta)} - 1 = 0. This would imply \zeta = 0 or a = -\beta \approx 0.02586. The scaled error term in F, which is the last term in the expression above, is E = -\mu \cdot e^{\lambda \cdot \zeta} = -\mu = -0.167. However, this is probably not a good idea since we have the 1/\zeta term which contradicts this solution.

Second: 1 + 2 / \zeta = 0. This would imply \zeta = -2 or a = -3 \cdot \beta \approx 0.07759. The scaled error term in F is now E = -\mu \cdot e^{-2 \cdot \lambda} \approx -0.456. That's probably a safer bet. However, since we underestimate F, we should probably bump up this value somewhat (ie, decrease \zeta somewhat away from -2).

Selecting \zeta = -3 yields a scaled value (1/100) \cdot F(-3) \approx 0.4301. We have now bracketed the root. A suggested initial value for an iteration routine would be \zeta^{(0)} \approx -2.5 (ie, a^{(0)} = 0.09052).

 

[END]

I don't see an analytical solution. For a numerical solution, consider the following:

Thank you for the in-depth explanation to a numerical approach, TheoMcCloskey! The technique you outlined is just beyond my current mathematical level of understanding, but it's educating to see a technique like that in action, and it's definitely brought up some points to research.

Does your approach have a specific name? I can't wait to study these concepts in the future.