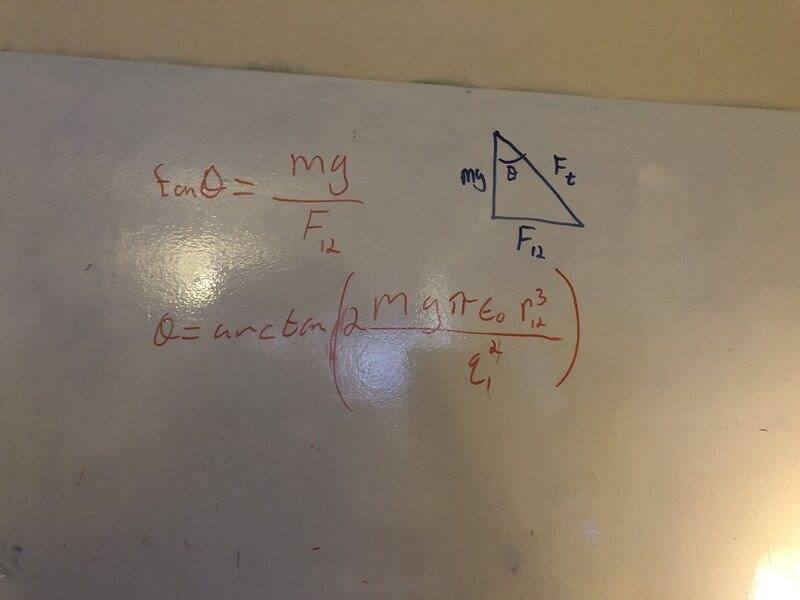Homework Help Overview
The discussion revolves around a problem in electromagnetic theory, specifically involving forces between charged masses and their equilibrium conditions. Participants are examining the correctness of a solution and the underlying equations related to forces, angles, and distances in the context of the problem.
Discussion Character
- Exploratory, Assumption checking, Mathematical reasoning
Approaches and Questions Raised
- Participants are checking the validity of equations and assumptions related to forces acting on charged masses. There are discussions about the correct use of variables, the significance of certain terms, and the implications of limits in the context of the problem. Some participants are attempting to clarify relationships between angles and distances in their equations.
Discussion Status
The discussion is ongoing, with participants providing feedback on each other's equations and reasoning. Some have offered corrections and suggestions for improvement, while others are exploring different interpretations of the problem. There is a collaborative effort to refine the understanding of the relationships involved.
Contextual Notes
Participants note the importance of expressing answers in terms of given quantities, such as the length of the string, rather than unknown variables. There are also mentions of issues with formatting equations and the need for clearer diagrams to represent the problem accurately.