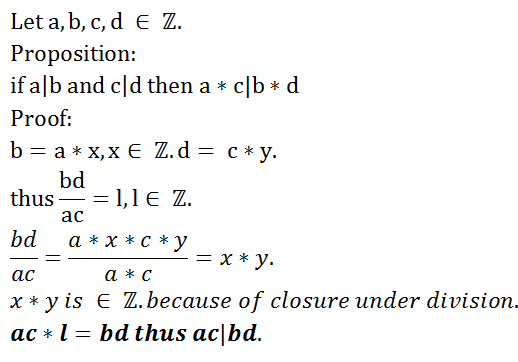The order of your proof needs work. You say
"Thus ##\frac{bd}{ac} = l, l \in \mathbb{Z}##"
Then you talk some more about ##\frac{bd}{ac}##, which should come before saying, "Thus..."
Here's what I think is a more direct proof:
a | b and c | d
Then b = ka and d = mc, for integers k and m.
So bd = kmac
Hence ac | bd.
When we say that a number a divides another b, both numbers are assumed to be integers, and a is assumed to be nonzero.
In the future, please post your work here directly, rather than as an image. Everything you did can be done using TeX. If you are uncertain how to use this, take a look at our tutorial, under INFO --> Help/How-tos. The LaTeX tutorial is listed there.