Is this question solvable by resolution of forces?

[Physical_Fire]

Homework Statement

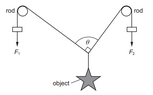
An object hangs by means of two cords around two rods, as shown. The object is held in equilibrium by the forces F1 and F2. The object weighs 10N. There is negligible friction between the rods and cords. Angle θ is 90°. What are the values of F1 and F2?

*Hint: Both the forces are different in magnitude.

Relevant Equations

Fx = Fcos(θ)
Fy = Fsin(θ)

Hello,
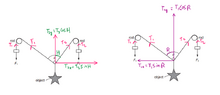
I have tried to resolve this using the fact that we consider the weight to be normal, so I resolved the tensions in both the strings using an angle of 45 degrees. Upon solving these simultaneously T2*cos(45) + T1*cos(45) - 10 = 0 , T2*sin(45) - T1*sin(45) = 0, I have gotten T1 = 5√2 and T2 = 5√2. And as T1 = T2, thus: F1 = 5√2 and F2 = 5√2. However using the hint guidance provided this is incorrect as they are the same. Can anyone show me the right way and where I have gone wrong?

 

[Steve4Physics]

I have tried to resolve this using the fact that we consider the weight to be normal,

I guess you mean vertical ('normal' means something different).

so I resolved the tensions in both the strings using an angle of 45 degrees. Upon solving these simultaneously T2*cos(45) + T1*cos(45) - 10 = 0 , T2*sin(45) - T1*sin(45) = 0, I have gotten T1 = 5√2 and T2 = 5√2. And as T1 = T2, thus: F1 = 5√2 and F2 = 5√2. However using the hint guidance provided this is incorrect as they are the same. Can anyone show me the right way and where I have gone wrong?

Looks like you have assumed the 2 sloping string-sections are both 45∘ to the vertical - which is wrong; if you don't understand why, you need to revise what it means to resolve a vector into components.

You don't know the 2 angles (only the fact that they add up to 90∘).

Your first step is to ask yourself: what are the tensions in the left and right strings? Remember, each string passes over a (presumably frictionless) rod.

 

[Physical_Fire]

Is this correct now?

 

[kuruman]

Draw a vector addition diagram showing how the three forces acting on the knot add to give zero. Do you see that they form a right triangle?

 

[Steve4Physics]

Is this correct now?

Yes - but resolving into components won't help. Use @kuruman's approach in Post #4.

 

[erobz]

Yes - but resolving into components won't help. Use @kuruman's approach in Post #4.

$F_1$ and $F_2$ are both variable. So I still think we have to use $\sum F_x = 0 \sum F_y = 0$, in conjunction to post 4 to land this one (three variables-three equations)?

If I'm missing something, I'll wait to see what the OP figures out.

 

[Physical_Fire]

Draw a vector addition diagram showing how the three forces acting on the knot add to give zero. Do you see that they form a right triangle?

Unfortunately, I don't understand your statement. Why cant we use system of equations to get the answers?

 

[Steve4Physics]

Worth noting that (unless I'm mistaken) the problem has a serious error. There are no unique solutions for $F_1$ and $F_2$. But there is a unique relationship between $W, F_1$ and $F_2$.

 

[gleem]

There are four unknowns which require four equations to determine them.

 

[erobz]

Unfortunately, I don't understand your statement. Why cant we use system of equations to get the answers?

How many variables do you see and how may equation do you have to utilize? I think there are some issues, even if we use post 4 because I get some nonsense when I try to use the three (suggested) equations.

 

[erobz]

There are four unknowns which require four equations to determine them.

I count 3 unknowns.

 

[gleem]

F1, F2, α, β

 

[erobz]

F1, F2, α, β

ok, I think I'm using a relationship for $\alpha, \beta$ implicitly i.e. $\alpha + \beta = \frac{\pi}{2}$. So there are initially 4.

Do you think there are issues with the problem as stated too or is that just me missing something?

 

[Steve4Physics]

With the parameters given, the relationship between $W, F_1$ and $F_2$ is easily shown to be $W^2 = F_1^2 + F_2^2$.

From the diagram, we see $F_2>F_1$. Since $W = 10N$, two of the (infinitely many) solutions are, for example:
$F_1 = 6N$ and $F_2 = 8N$ (Edit - this is the only integer solution.)
$F_1 = \sqrt {19}N$ and $F_2 = 9N$

Each solution has diffferent values for $\alpha$ and $\beta$ but $\alpha + \beta$ always equals 90$^\circ$.

The question is faulty!

 

[Physical_Fire]

@Steve4Physics All of your solutions are correct as per the instructor's answer scheme. Mind sharing how you found them out?

 

[Physical_Fire]

With the parameters given, the relationship between W,F1 and F2 is easily shown to be W2=F12+F22.

How do you know that T1 = F1 and T2=F2?

 

[Steve4Physics]

@Steve4Physics All of your solutions are correct as per the instructor's answer scheme. Mind sharing how you found them out?

Using components is not always the best or most approppriate way to add vectors. I used a vector addition triangle. A lesson on vector addition wouldn't be appropriate here, but consider this:

Can you apply this method to the original question?

 

[Steve4Physics]

How do you know that T1 = F1 and T2=F2?

Examine the forces acting on each object at the side. And remember tension will be constant along each string as the rods are frictionless.

 

[Physical_Fire]

Examine the forces acting on each object at the side. And remember tension will be constant along the string as the rods are frictionless.

Can we prove it mathematically that they are equal? My issue is not drawing a vector diagram but rather knowing that the tensions are equal to the F's

 

[Steve4Physics]

Consider a

Can we prove it mathematically that they are equal? My issue is not drawing a vector diagram but rather knowing that the tensions are equal to the F's

No maths is needed! Consider, say, the object hanging on the left.

$F_1$ is the magnitude of the total downwards force on the object (it will include the object's weight).
$T_1$ is the magnitude of the total upwards force on the object.

The object is in equilibrium, therefore we know that... [complete the sentence for yourself!].

 

[Physical_Fire]

Hmm yeah. Makes sense. Thank you all.

 

[kuruman]

Unfortunately, I don't understand your statement. Why cant we use system of equations to get the answers?

Because it's more complicated. If you consider that the sum of forces can be represented as a closed triangle, you will see immediately that there is no unique solution.

Look at the figure figure below. On the left you have the two vectors (bold means magnitude and direction) $\mathbf T_1$ and $\mathbf T_2$ at right angles to each other and with their tails together. To find their sum, slide $\mathbf T_2$ parallel to itself until its tail is at the tip of $\mathbf T_1$. Then the sum of the two vectors has magnitude equal to the hypotenuse of the right triangle.

The sum of the three forces acting on the knot must be zero, $$ \mathbf T_1+\mathbf T_2+m\mathbf g=0$$which says that the hypotenuse must be equal to the weight, $mg=10~$N. Thus $$\sqrt{T_1^2+T_2^2}~=10~\text{N}.$$How many ways are there to add the squares of two numbers, take the square root and get 10?

 

[haruspex]

How many ways are there to add the squares of two numbers, take the square root and get 10?

Depends what sort of number you allow, natural, integer, rational, algebraic, real, complex..?