Junction affects the flow of water?

[foo9008]

Homework Statement

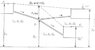
based on this picture in the notes , the author gave that if D is below B , then h2 and Q2 = 0 , what dos it mean ? what does it mean ? water cannot flow out and in from B ?
please ignore the pencil sketched-part

Homework Equations

The Attempt at a Solution

 

[BvU]

Hey, there is D ! Doesn't this look a lot like the other thread ?
But this time there is no $h_2$ (or no $h_{f2}$ ?
Could you merge the threads and try to get completeness ?
Or should I ask a mentor ?

What exactly are the litteral words the author uses ? Because D is definitely below B as anyone can see. At least if the top of the picture represents 'up'.

 

[haruspex]

@foo9008, in past threads on this, or very similar problems, the solution technique was iterative. You could start with arbitrary assumptions about flows and iteratively adjust them until the correct solution emerged. Are you sure that is not what the author is doing here, assuming Q2 to be zero as a first guess?
If you don't think that is the explanation, please post the exact text.

 

[foo9008]

@BvU and @haruspex , here's the full text , can you explain about the author gave that if D is below B , then h2 and Q2 = 0 , what dos it mean ? what does it mean ? water cannot flow out and in from B ?
no , this is just notes , while in the another thread is just the sample problem which shares the same diagram with the notes

 

[haruspex]

@BvU and @haruspex , here's the full text , can you explain about the author gave that if D is below B , then h2 and Q2 = 0 , what dos it mean ? what does it mean ? water cannot flow out and in from B ?
no , this is just notes , while in the another thread is just the sample problem which shares the same diagram with the notes

The text is clearly inconsistent, so there must be a typo. I suggest that the first one should read "if P is at the same height as B". (And I assume the author is using P and D interchangeably.)

 

[foo9008]

The text is clearly inconsistent, so there must be a typo. I suggest that the first one should read "if P is at the same height as B". (And I assume the author is using P and D interchangeably.)

ok , do you mean it should be when D is same height as B , no water will flow out , so Q2 and h2 = 0 ?

 

[foo9008]

@haruspex , the last statement is also wrong , am i right ? it stated that when P is below B , the water is definitely out of B , so Q1 + Q2 = Q3 ?
but , it also can be water from A flow into B and C which means (Q1 = Q2 + Q3) ?
depending on the situations , am i right ?

 

[haruspex]

@haruspex , the last statement is also wrong , am i right ? it stated that when P is below B , the water is definitely out of B , so Q1 + Q2 = Q3 ?
but , it also can be water from A flow into B and C which means (Q1 = Q2 + Q3) ?
depending on the situations , am i right ?

I agree that intuitively it could flow down from C, but if viscosity is being ignored then intuition may mislead. I need to think about it some more.
Have you tried analysing it using Bernoulli?

 

[foo9008]

I agree that intuitively it could flow down from C, but if viscosity is being ignored then intuition may mislead. I need to think about it some more.
Have you tried analysing it using Bernoulli?

i think you mean B ? do you mean if the viscocsty is ignore , then the intuition of water from a can flow up to C is correct ?

 

[haruspex]

i think you mean B ? do you mean if the viscocsty is ignore , then the intuition of water from a can flow up to C is correct ?

Yes, B. I mean if there is viscosity then I expect it can flow up to B, but without viscosity I'm not sure.

 

[foo9008]

Yes, B. I mean if there is viscosity then I expect it can flow up to B, but without viscosity I'm not sure.

so , by saying that when P is below B , the water is definitely out of B , so Q1 + Q2 = Q3 , the author assuming water has no viscosity , so the water can't flow from A up to C ?

 

[haruspex]

so , by saying that when P is below B , the water is definitely out of B , so Q1 + Q2 = Q3 , the author assuming water has no viscosity , so the water can't flow from A up to C ?

That's what the author is saying, but I don't know how that is shown.

 

[BvU]

Messy threads, this one and the -- 98% identical to this one -- other thread which I find a lot more sensible.
The note in post #4 here clarifies a few things -- and messes up others.

• Haru fixed the first 'If P is below' which should have been 'at'.
• The term 'elevation of P' confused me no end

I'm not used to working in terms of 'head', only with pressure, but I think 'elevation of P' is the same as $H_J$ and then $P_D$ is understandably the pressure at D .
What P is I find declared nowhere (whatever happened to 'all variables and given/known data' in the template -- my addition: including the dimensions ) ?
That would make for $\ \ H_J = P = Z_D + P_D/(\rho g)\ \$ (so not $\ \ Z_D + P_D/\rho \; g \ \$, nitpicking, I know) and now I'm still a bit dazzled but back in the race.​

• 'the pipes are sufficiently long that we can neglect minor losses and velocity head' also is cryptic to me. long ? or wide ? The idea is to ignore friction loss (viscosity = 0) ? But why ignore 'velocity head' - when $V^2/g$ is featuring clearly in the other thread ? Or is velocity head something else than this term from the Bernoulli equation ?

@haruspex, could you look at the other thread, see if it is identical and if so, see if the combination makes sense ?

 

[haruspex]

Messy threads, this one and the -- 98% identical to this one -- other thread which I find a lot more sensible.
The note in post #4 here clarifies a few things -- and messes up others.

• Haru fixed the first 'If P is below' which should have been 'at'.
• The term 'elevation of P' confused me no end

I'm not used to working in terms of 'head', only with pressure, but I think 'elevation of P' is the same as $H_J$ and then $P_D$ is understandably the pressure at D .
What P is I find declared nowhere (whatever happened to 'all variables and given/known data' in the template -- my addition: including the dimensions ) ?
That would make for $\ \ H_J = P = Z_D + P_D/(\rho g)\ \$ (so not $\ \ Z_D + P_D/\rho \; g \ \$, nitpicking, I know) and now I'm still a bit dazzled but back in the race.​

• 'the pipes are sufficiently long that we can neglect minor losses and velocity head' also is cryptic to me. long ? or wide ? The idea is to ignore friction loss (viscosity = 0) ? But why ignore 'velocity head' - when $V^2/g$ is featuring clearly in the other thread ? Or is velocity head something else than this term from the Bernoulli equation ?

@haruspex, could you look at the other thread, see if it is identical and if so, see if the combination makes sense ?

I might be starting to get what is going on here. As you say, we have no definition of P. I was taking it to be interchangeable with D, but I now think it is an energy level associated with D.
The diagram in the other thread shows the physical arrangement of pipes, plus a schematic "energy line". Note that the slopes are not the same between the two. In the schematic there is an energy level H_J associated with the junction.
There is a similar energy diagram in the current thread, this time using dashed lines. I suggest "P" in the text refers to the energy level at D. If this is equal to that at B then there is no flow to or from B, etc. That makes sense.

Now, none of these diagrams can be handled with simple Bernoulli. Either there is viscosity or the flows will accelerate. I'm not sure which of those the author assumes, maybe it doesn't matter.