Delta_Craig
- 5
- 4
- Homework Statement
- Self study
I just ran this pretty quick at work. But this is the general outline. Sorry for the slop, it will get better with time. Thanks in advance and any additional info can be supplied.
The material is from the Khan free course.
.....
A student is fed up with doing her kinematic formula homework, so she throws her pencil straight upward at 18.3 m/s.
How long does it take the pencil to first reach a point 12.2 m higher than where it was thrown?
Answers are suppose to be
t1= 0.869s
t2= 2.86s
My answers are negative time which is a neat concept. Doesn’t add up.
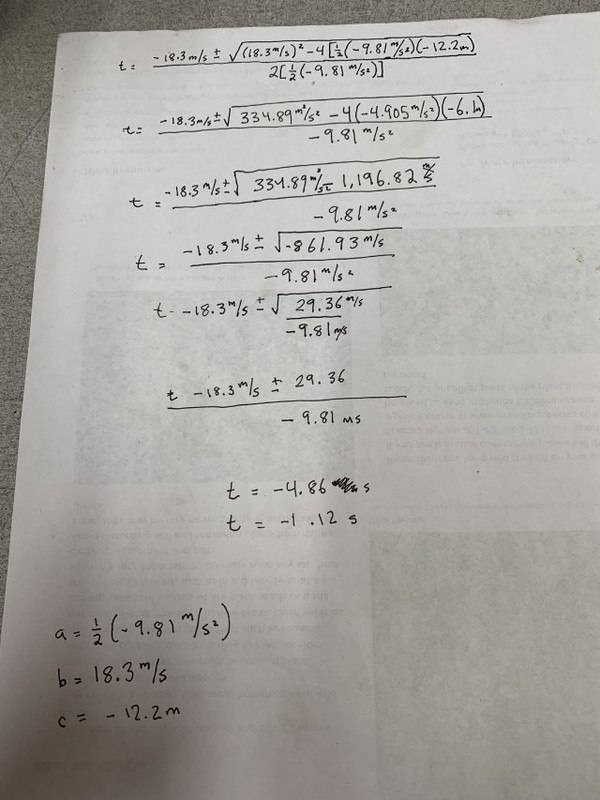
The material is from the Khan free course.
.....
A student is fed up with doing her kinematic formula homework, so she throws her pencil straight upward at 18.3 m/s.
How long does it take the pencil to first reach a point 12.2 m higher than where it was thrown?
Answers are suppose to be
t1= 0.869s
t2= 2.86s
My answers are negative time which is a neat concept. Doesn’t add up.