Physics_learner
- 1
- 0
- Homework Statement
- Kinematics - finding the initial velocity and final x position
- Relevant Equations
- x(t)=x0+v0*(t2-t1)+0.5a*(t2-2a)^2
v(t)=v0+a*(t2-t1)
I tried to write the data I understood from the image:
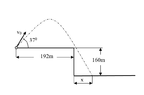
y0=160m
yf=0
x0=0
x1=192m
I tried to express the total change in time using the position over time equation on the Y direction:
y(t)=y0+v0y*(t2-t1)-0.5a(t2-t1)^2
but then I stuck with 2 variables and didn't know what to do
any help?
y0=160m
yf=0
x0=0
x1=192m
I tried to express the total change in time using the position over time equation on the Y direction:
y(t)=y0+v0y*(t2-t1)-0.5a(t2-t1)^2
but then I stuck with 2 variables and didn't know what to do
any help?