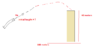Projectile Motion with Unknown Initial Height

In summary, the conversation discusses solving for the time of flight and maximum height of a projectile and the different approaches that were attempted. The problem also explores the possibility of hitting a target at a certain distance and the implications of changing the initial velocity and target distance.
  • #1
a1234
78
6
Homework Statement
I am given a problem where a 6kg object is launched from a cannon from an unknown initial height and eventually lands on top of a platform that is at a height of 40 meters above the ground. As you can see from the diagram, the final height is greater than the initial height.

The total displacement in the x-direction is 100 meters, and the object is launched from an angle of 25 degrees with an initial velocity of 5 m/s. I am asked to find the initial height at which the object is launched.
Relevant Equations
y=y0+vy0(t)-1/2gt^2,x=x0+vx0(t),v=v0+at, vy^2 = vy0^2-2g*change in y
First, I tried solving for the total time of flight, which I got as 100 = 5cos25*t --> t=22 s
Since we know the height at which the object lands, but not at which it is launched, I tried setting up the equation as:
yf = 40 - y0 = y0 + 5sin25*(22) - 1/2(9.8)(22)^2
However, I got y0 = 1183 m, which is not realistic given the problem statement. I assume this equation works if we only have freefall from an initial height.

I then tried solving for the the height at which vy = 0 (at max height):
0^2 = (5sin25)^2-2*9.8*deltay
delta y = 0.23 m

I also tried vy = v0y - gt for vy = 0 and got t = 0.22 s.

I don't know where to proceed from there. I also don't know if we need to change the sign of acceleration due to gravity when we consider motion past the point of maximum height.
 

Attachments

  • ProjectileMotion Problem.PNG
    ProjectileMotion Problem.PNG
    1.9 KB · Views: 303
Physics news on Phys.org
  • #2
Do you think you can hit a target 100m away by launching a projectile at 5m/s?
 
  • #3
What would be the approach to solving the problem if the target were not as far away?
 
  • #4
a1234 said:
What would be the approach to solving the problem if the target were not as far away?
Your answer of over 1000m might well be correct!
 
  • #5
a1234 said:
What would be the approach to solving the problem if the target were not as far away?

You could try with ##v_0 = 50m/s##.
 
  • #6
With v0 = 50 m/s, I get y0 = 973 m, which still doesn't meet the criterion that y0 < yf.

I have a very similar problem with v0 = 8 m/s, θ = 35 degs, x = 7 m, yf = 3 m, and mass of object = 2 kg. I'm having the same problem with that too.
 
  • #7
a1234 said:
With v0 = 50 m/s, I get y0 = 973 m, which still doesn't meet the criterion that y0 < yf.

That is definitely not right. What's your time of flight?

a1234 said:
With v0 = 50 m/s, I get y0 = 973 m, which still doesn't meet the criterion that y0 < yf.

I have a very similar problem with v0 = 8 m/s, θ = 35 degs, x = 7 m, yf = 3 m, and mass of object = 2 kg. I'm having the same problem with that too.

One problem at a time!
 
  • #8
Oops...I used the same time of flight as for the previous problem.

The new time is 100 = 50cos25 * t ---> t = 2.2 s
So, 40 - y0 = y0 + 50sin25*2.2 - 1/2(9.8)(2.2)^2 --> y0 = 8.6 m
 

FAQ: Projectile Motion with Unknown Initial Height

1. What is projectile motion?

Projectile motion is the motion of an object through the air or space under the influence of gravity. It follows a curved path known as a parabola.

2. What is the formula for calculating projectile motion with unknown initial height?

The formula for calculating projectile motion with unknown initial height is:
h = (v2sin2θ)/2g, where h is the height, v is the initial velocity, θ is the angle of projection, and g is the acceleration due to gravity.

3. How do you determine the initial velocity of a projectile with unknown initial height?

To determine the initial velocity of a projectile with unknown initial height, you can use the horizontal and vertical components of the velocity. The horizontal component can be found using the formula: vx = vcosθ, and the vertical component can be found using the formula: vy = vsinθ. Once you have both components, you can use the Pythagorean theorem to find the magnitude of the initial velocity.

4. How does initial height affect the trajectory of a projectile?

The initial height affects the trajectory of a projectile by changing the starting point of the motion. If the initial height is higher, the projectile will have a longer flight time and a longer range. However, the shape of the trajectory will still be a parabola.

5. What factors can affect the accuracy of calculating projectile motion with unknown initial height?

Some factors that can affect the accuracy of calculating projectile motion with unknown initial height include air resistance, wind, and the precision of the measurements taken. Other factors such as the shape and weight of the object, as well as the surface it is launched from, can also affect the trajectory and accuracy of the calculations.

Similar threads

Projectile Motion Problem Involving Initial Velocity and Gravity Only
Replies
11
Views
634
Find Projectile Flight Time Given Only Maximum Height
Replies
4
Views
2K
Kinematics - can't find the initial velocity according to the image
Replies
2
Views
1K
Initial Position Discrepancy Involving Fluid Resistance
Replies
5
Views
1K
Relationship between Launch height and range of a projectile
Replies
15
Views
22K
A ball is thrown w/initial speed vi at an angle 𝜃i with the horizontal
Replies
5
Views
729
Calculation of Ramp Jump Distance Using Projectile Motion Formulas?
Replies
12
Views
494
Projectile Motion Problem: Maximum Height of a Ball Shot into the Air
Replies
11
Views
2K
Projectile motion with (constant) wind velocity
Replies
8
Views
2K
Projectile Motion Equation: Calculating Height from Initial Velocity and Time
Replies
3
Views
1K

Hot Threads

Recent Insights

Back
Top