- #1
Avatrin
- 245
- 6
Hi
Let's look at this:
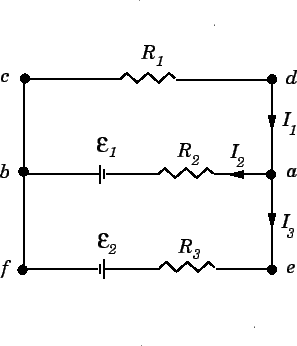
The issue I am having is that while I know that this is accurate:
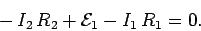
I just cannot wrap my head around why. I1 is a result of both voltage sources. So, while the equations clearly tell me that the voltage drop across the resistor R1 is I1R1, I cannot wrap my head around how this works in terms of Kirchoff's loop rule.
Let's look at this:
The issue I am having is that while I know that this is accurate:
I just cannot wrap my head around why. I1 is a result of both voltage sources. So, while the equations clearly tell me that the voltage drop across the resistor R1 is I1R1, I cannot wrap my head around how this works in terms of Kirchoff's loop rule.