Lindsayyyy
- 215
- 0
Hi
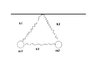
Look at the drawing. Furthermore I have a constant acceleration \vec g = -g \hat y
I shall find the Lagrange function and find the equation of motion afterwards.
Lagrange/ Euler function and eqauation
I found out the following for the kinetic energy and the potential energy:
T=\frac {1} {2} m_{1} \dot{\vec r_{1}}^{2} + \frac {1} {2} m_{2} \dot{\vec r_{2}}^{2}
and for the potential energy:
V=\frac 1 2 k_{1}{\vec r_{1}}^{2}+\frac 1 2 k_{2} {\vec r_{2}}^{2}+m_{1}gy_{1}+m_{2}gy_{2}+\frac 1 2 k_{3}({\vec r_{1}}-{\vec r_{2}})^{2}
Now I used the Euler- Lagrange equation of motion and found out that:
m_{1}\ddot{\vec r_{1}}=-k_{1}{\vec r_{1}}+k_{3}{\vec r_{1}}-m_{1}g\hat y
and
m_{2}\ddot{\vec r_{2}}=-k_{2}{\vec r_{2}}-k_{3}{\vec r_{2}}-m_{2}g\hat y
Can anyone confirm this? Or did I do any mistakes?
Thanks for your help
Homework Statement
Look at the drawing. Furthermore I have a constant acceleration \vec g = -g \hat y
I shall find the Lagrange function and find the equation of motion afterwards.
Homework Equations
Lagrange/ Euler function and eqauation
The Attempt at a Solution
I found out the following for the kinetic energy and the potential energy:
T=\frac {1} {2} m_{1} \dot{\vec r_{1}}^{2} + \frac {1} {2} m_{2} \dot{\vec r_{2}}^{2}
and for the potential energy:
V=\frac 1 2 k_{1}{\vec r_{1}}^{2}+\frac 1 2 k_{2} {\vec r_{2}}^{2}+m_{1}gy_{1}+m_{2}gy_{2}+\frac 1 2 k_{3}({\vec r_{1}}-{\vec r_{2}})^{2}
Now I used the Euler- Lagrange equation of motion and found out that:
m_{1}\ddot{\vec r_{1}}=-k_{1}{\vec r_{1}}+k_{3}{\vec r_{1}}-m_{1}g\hat y
and
m_{2}\ddot{\vec r_{2}}=-k_{2}{\vec r_{2}}-k_{3}{\vec r_{2}}-m_{2}g\hat y
Can anyone confirm this? Or did I do any mistakes?
Thanks for your help