- #1
GrimGuy
- 11
- 2
Hey guy,
I'm having problems to understand the final part of this section. The book says we have the lagrangian from one particle (106.16), then we have some explanation and then the total lagrangian is given(106.17). For me is everything fine until the 106.16, then i couldn't get what is going on. What I've tried to do is, I've substituted the ##h_{00}##, ##h_{0\alpha} ##, ##h_{\alpha \beta } ## and ##\phi##, ##\phi_{a}## into 106.16 and tried to find 106.17 (no sucsses). Any enlightenment on this will be extremely appreciated.
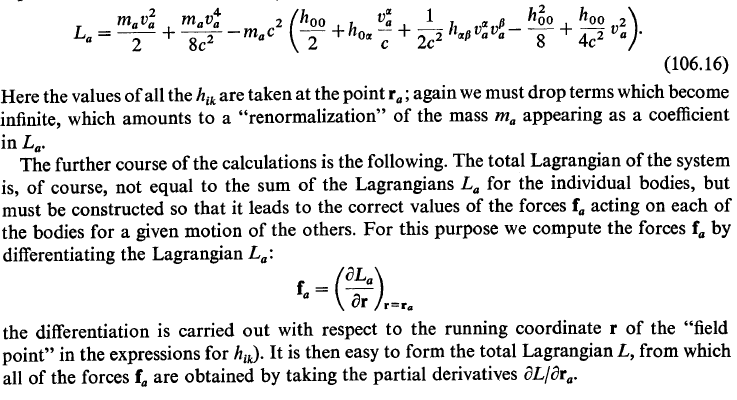

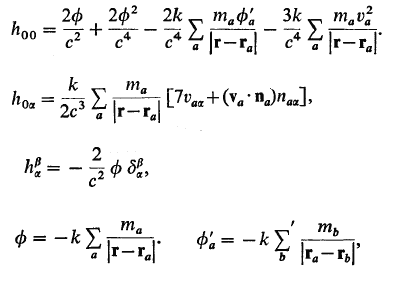
I'm having problems to understand the final part of this section. The book says we have the lagrangian from one particle (106.16), then we have some explanation and then the total lagrangian is given(106.17). For me is everything fine until the 106.16, then i couldn't get what is going on. What I've tried to do is, I've substituted the ##h_{00}##, ##h_{0\alpha} ##, ##h_{\alpha \beta } ## and ##\phi##, ##\phi_{a}## into 106.16 and tried to find 106.17 (no sucsses). Any enlightenment on this will be extremely appreciated.