- #1
rouge89
- 2
- 0
I am wondering, how does lagrangian of such system look like?
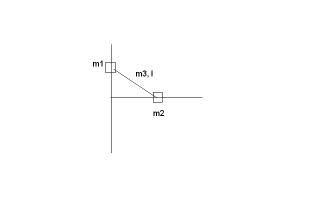
Will it be:
[tex]L=\frac{m_{1} \cdot \dot{y}^2}{2} + \frac{m_{2} \cdot \dot{x}^2}{2} +\frac{m_{3} \cdot (\dot{y'}^2+\dot{x'}^2)}{2} + \frac{I \cdot \dot{ \alpha }^2}{2} - mgy - mgy' [/tex]
where:
[tex]y'=\frac{l}{2}sin(\alpha) [/tex]
[tex]x'=\frac{l}{2}cos(\alpha) [/tex] ?
Will it be:
[tex]L=\frac{m_{1} \cdot \dot{y}^2}{2} + \frac{m_{2} \cdot \dot{x}^2}{2} +\frac{m_{3} \cdot (\dot{y'}^2+\dot{x'}^2)}{2} + \frac{I \cdot \dot{ \alpha }^2}{2} - mgy - mgy' [/tex]
where:
[tex]y'=\frac{l}{2}sin(\alpha) [/tex]
[tex]x'=\frac{l}{2}cos(\alpha) [/tex] ?