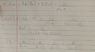- #1
Cocoleia
- 295
- 4
Homework Statement
I am given this equation:
and asked to solve using Laplace transforms
The Attempt at a Solution
This is what I did:
This seemed logical to me, I used partial fractions and it stayed pretty simple.
This is what the solutions my prof posted do:
Is my answer equivalent to this, or are their faults in my logic and work ?