breid040
- 9
- 1
- Homework Statement
- How does L change as mb gets heavier?
- Relevant Equations
- d=m(L/2)/(sqrt((2M)^2-(m)^2))
Hello all,
I am working on a lab report for physics, and am a bit stuck on one aspect. The basic layout of the pulley system is attached. (This is a diagram I made, so if there are any inaccuracies in this one either, I am happy to fix it.

So, I mostly understand the lab. My TA said, though, that L/2 changes as more weight is added onto mb.
Here is my attempt at understanding why:
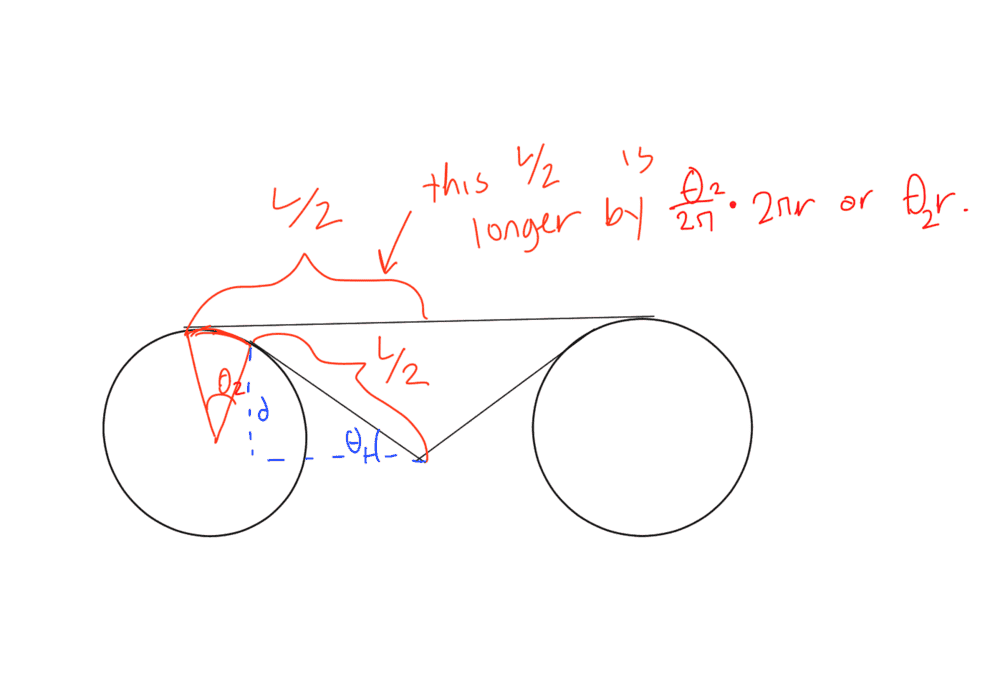
Is this accurate? I just wanted to check.
I am working on a lab report for physics, and am a bit stuck on one aspect. The basic layout of the pulley system is attached. (This is a diagram I made, so if there are any inaccuracies in this one either, I am happy to fix it.
So, I mostly understand the lab. My TA said, though, that L/2 changes as more weight is added onto mb.
Here is my attempt at understanding why:
Is this accurate? I just wanted to check.