- #1
VladZH
- 56
- 1
It is known that light beam bends near massive body and the object sendind deflected the beam is seen in shifted position.
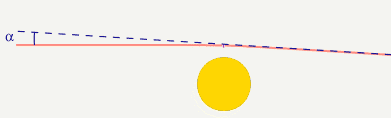
Now about spacetime curvature. As I undestand the things are like that:
http://i11.pixs.ru/storage/3/3/4/pic2png_7037348_21446334.png
The question is why are geodesics in left side not the same as in right? So I'd expect this situation
http://i10.pixs.ru/storage/4/5/6/pic3png_9235518_21446456.png
So that we can see objects before the body without shifting
Now about spacetime curvature. As I undestand the things are like that:
http://i11.pixs.ru/storage/3/3/4/pic2png_7037348_21446334.png
The question is why are geodesics in left side not the same as in right? So I'd expect this situation
http://i10.pixs.ru/storage/4/5/6/pic3png_9235518_21446456.png
So that we can see objects before the body without shifting
Last edited by a moderator: