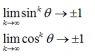YoshiMoshi said:
Homework Statement
The picture attached appeared in my powerpoint for my class. It's been a long time since I took calculus 1, but if I remember correctly this formula is wrong correct?
I mean thinking about it
limit k-> inf ( cos(theta)^k ) = 0 if theta is not a multiple of pi OR +/- 1 if theta is a multiple of pi
limit k-> inf ( sin(theta)^k ) = 0 if theta is not a multiple of pi/2 OR +/- 1 if theta is a multiple of pi/2
I don't see how the generic formula is correct since domain of theta was not provided.
Thanks in advance.
Homework Equations
The Attempt at a Solution
You are more-or-less on the right track, but some of your details need tightening up. First, it is enough to assume ##0 \leq \theta < 2 \pi##, because ##\sin## and ##\cos## are periodic, with period ##2 \pi##.
Looking at ##\sin \theta##, the limit ##\lim_{k \to \infty} \sin^k \theta = 0 ## whenever ##|\sin \theta | < 1##, so whenever ##\theta \neq \pi/2, 3\pi/2.## At ##\theta = \pi/2## we have ##\sin(\pi/2) = 1##, so ##\sin^k (\pi/2) \to 1## as ##k \to \infty##. However, ##\sin(3\pi/2) = -1##, so ##\sin^k (3 \pi/2) = (-1)^k## does not have a limit as ##k \to \infty##. It is 100% wrong to say that the limit is ##\pm 1## in this case: it isn't, there is no limit!.
You can do the same type of thing for ##\cos \theta ##.
BTW: to avoid trouble, you need to assume that ##k \to \infty## through integer values, because if ##k## is just some large real number, using it as a power could involve taking fractional powers of negative numbers, and that can get tricky.
