Line charge within a charged shell (basket case)

[hashbrowns808]

1. Homework Statement
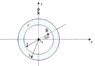
An infinite line of charge with linear density λ1 = 6.8 μC/m is positioned along the axis of a thick insulating shell of inner radius a = 2.5 cm and outer radius b = 4.8 cm. The insulating shell is uniformly charged with a volume density of ρ = -667 μC/m3.

1) What is λ2, the linear charge density of the insulating shell?

-3.518247622μC/m

2) What is Ex(P), the value of the x-component of the electric field at point P, located a distance 8.1 cm along the y-axis from the line of charge?

0 N/C

3) What is Ey(P), the value of the y-component of the electric field at point P, located a distance 8.1 cm along the y-axis from the line of charge?

This is where I'm stuck.

Homework Equations

Gauss' law ∫E⋅dA=Q_enc/∈
I know there will be integrations in there but due to a week of snow days the instructor hasn't covered any of that, so I'm not sure if there is something else I'm missing, and I'm not finding any good material that I can extract something from.

The Attempt at a Solution

The first section to the homework was similar, but with a conducting shell. I figured that out with the help of Michael Van Biezen videos, but I don't get how to use charge densities, or how to integrate what.

E∫(πR²)L = ∫dQ/∈ (I'm using ∈ for epsilon naught)
dQ=λdV
dV=∫(from a-b)πL(R_a²-R_b²)
dQ=λπL∫(R_a²-R_b²)
EπR² = (λπL∫(R<sub>a[/SUB2]-Rb²))/∈
E = (λL∫a^b(Ra²-Rb²))/R∈

That's what I have written on my paper. I'm just totally lost and desperate at this point. Like I said my teacher is expecting way too much without much instruction, and I'm sorry for short comings, but I just really need help.

Thanks!</sub>

 

[marchcha]

Ey(P) = 2*k(this is 9.0E9)*(Charge density of outer shell * area of outer cylinder + lambda of line) all divided by radius (.081m) let me know if this works out for you

 

[marchcha]

Ey(P) = 2*k(this is 9.0E9)*(Charge density of outer shell * area of cylinder (use length 1) + lambda of line) all divided by radius (.081m) let me know if this works out for you

******length of one is not even needed disregard that

 

[hashbrowns808]

******length of one is not even needed disregard that

I got:

E_y(P) =( 2(8.99810^9)(-667π(.048²-.025²))/.081
= -780964101685
and it was incorrect.

 

[marchcha]

I got:

E_y(P) =( 2(8.99810^9)(-667π(.048²-.025²))/.081
= -780964101685
and it was incorrect.

what you are trying to do in this problem is act like the system is a point charge so take the lambda you found in the beginning and add it to the lambda given multiply it by two and k and then divide by the radius (0.081)

 

[hashbrowns808]

what you are trying to do in this problem is act like the system is a point charge so take the lambda you found in the beginning and add it to the lambda given multiply it by two and k and then divide by the radius (0.081)

Ok so (((6.8x10^-6)+(-3.518x10^-6))2(8,99x10^9))/.081
=728522.9629

Got it. Thank you so much! I think I'll have to work out that integral backwards.
I'm asking this before I've figured out how to arrive at the formula you gave me, but why can I treat it as two point charges? The x components of the shell cancel, and y components < 0 (along y axis), is it just that the y-comp fields end up averaging to λ₁? Does anyone know of a good link where I can learn more about this?

I use Flipit physics, and I find it difficult to follow at best, and like I said we're cramming 3 sections into 1 week, where we'd normally be doing half that, and the teacher hasn't been able to give us much help.

Again thanks Marchcha for the help.

 

[marchcha]

Ok so (((6.8x10^-6)+(-3.518x10^-6))2(8,99x10^9))/.081
=728522.9629

Got it. Thank you so much! I think I'll have to work out that integral backwards.
I'm asking this before I've figured out how to arrive at the formula you gave me, but why can I treat it as two point charges? The x components of the shell cancel, and y components < 0 (along y axis), is it just that the y-comp fields end up averaging to λ₁? Does anyone know of a good link where I can learn more about this?

I use Flipit physics, and I find it difficult to follow at best, and like I said we're cramming 3 sections into 1 week, where we'd normally be doing half that, and the teacher hasn't been able to give us much help.

Again thanks Marchcha for the help.

Hey as a user of flipit physics I feel your pain. You treat it as two point charges because it is outside of the conductor.