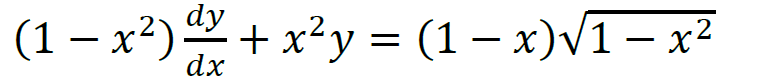mahmoud shaaban
- 4
- 0
Can i have help with this linear differential equation ?
First, i divided by (1-x^2) to be like dy/dx + p(x)y= q(x). But i could not obtain Q(x).
Any help will be welcomed.
View attachment 6473
First, i divided by (1-x^2) to be like dy/dx + p(x)y= q(x). But i could not obtain Q(x).
Any help will be welcomed.
View attachment 6473