Linearity and superposition theorem

[Ivan Antunovic]

Homework Statement

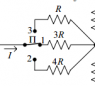
For the network of constant current shown in Figure 4 it is known that R1 = 50 Ω and , R = 10 Ω. When the switch P is
in the 1-position , current I = 50 mA and Ip = 70 mA known i . When the switch P is in
the 2-position , current I' = 40 mA and Ip' = 90 mA are known . Determine the current Ip''
when the switch switches to the third position.

Homework Equations

The Attempt at a Solution

By linearity and superposition theorem we have a linear network and if we have our active load network we can write I = xU + y , where current I is the response and voltage U represents excitation , constants x and y are determined by the resistance of the active network ,where x has dimension of A/V and y has dimension of A.

By solving equation 1 and equation 2 I get that,
x = 0.2 and y = -0.23,
for the 3rd equation I get:
Ip" = xU1 + y = 0.2 U1 - 0.23
I have two unknowns Ip" ,U1 and only 1 equation.
What am I doing wrong?

 

[cnh1995]

What if you put the parallel network of R, 3R and 4R inside the active network box? You know the value of R and currents I and I'. Is it possible to find I'' using the same method you used above? I am not sure, it's just a suggestion. I'm not familiar with your method.

 

[Ivan Antunovic]

What if you put the parallel network of R, 3R and 4R inside the active network box? You know the value of R and currents I and I'. Is it possible to find I'' using the same method you used above? I am not sure, it's just a suggestion. I'm not familiar with your method.

It would only change constants x and y since the resistance of the active network would be changed , I would have form Ip = xI + y , where x would be non dimensional constant and y would be constant with dimension of amperes , still I would end up with 1 equation with 2 unknowns.

 

[Ivan Antunovic]

Hm if my logic is right

Answer should be for R I"p = 30 mA ?

 

[Ivan Antunovic]

@cnh1995
For example look at those simulations, imagine this network in the black box is the active network and you don't know what is in it ( active since it has active sources, if there were only resistors equation would have y = 0)

capture

Let the V1 be excertation and the voltage measured by the voltmeter be response V2 .
So for the first two pictures we have
V1 = 200 V , V2 = 14.3 V
V1 = 300 V , V2 = 28.6 V
V2 = xV1 + y , and solving this equation you get
x = 0.142 and y = -14

Now suppose you wanted to find the voltage for V1 = 400 V
you already know constants so it's
V2 = V1*0.142 -14 = 400 * 0.142 -14 = 42. 8 V .

Look at the picture below , we get 42.8 V the same result.

screen shot on windows
That is the whole idea about this theorem as I said if there were only resistors in the black box we would have constant y = 0 , so equation would look like V2 = x*V1 ,linear homonogeous equation.

 

[NascentOxygen]

Try writing I_p in terms of that switched resistance (I'll denote it R^* for convenience, i.e.,
I_p = kR^* + y

If you need to find I'' then determine I as a similar linear relationship to R^*.

 

[Ivan Antunovic]

Try writing I_p in terms of that switched resistance (I'll denote it R^* for convenience, i.e.,
I_p = kR^* + y

If you need to find I'' then determine I as a similar linear relationship to R^*.

70 m = x30 +y
90 m = x40 +y

x = 0.002 , y = 0.01

Ip" = xR + y = 0.002 * 10 + 0.001 = 30mA , may I ask you how did you come up with this?
I was thinking it could be since R becomes excitation and by compensation theorem
http://www.electrical4u.com/compensation-theorem/

if a current or voltage is known on the resistor it can be replaced by ideal voltage/current source and vice versa

 

[NascentOxygen]

The only independent variable (called "input") in this system is the switch position, i.e., the resistance R^❇. So it seemed that you should be looking for the linear relationship between output I_p and input R^*.

 

[Ivan Antunovic]

The only independent variable (called "input") in this system is the switch position, i.e., the resistance R^❇. So it seemed that you should be looking for the linear relationship between output I_p and input R^*.

By the way I think it's called proportionality theorem in english literature.