Jason-Li
- 119
- 14
Homework Statement
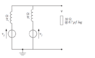
FIGURE 1 shows a 50 Ω load being fed from two voltage sources via
their associated reactances. Determine the current i flowing in the load by:
(a) applying Thévenin’s theorem
(b) applying the superposition theorem
(c) by transforming the two voltage sources and their associated
reactances into current sources (and thus form a pair of Norton
generators)
The Attempt at a Solution
(a)
Converting V1 & V2 to RMS values and V1 to a sin value:
V1 = 415sin(100πt+90)
V2 = 415sin(100πt)
and from Asin(ωt+Φ)
V1 = 415∠90V or 0+j415 V
V2 = 415∠0V or 415+j0 V
Then current around the circuit:
I =V/Z = (V2-V1) / (Z2+Z1) = (415-j415) / (j10)
This as a polar form division:
586.8986∠-45 / 10∠90 = 58.68986∠-135 A or -41.5-j41.5
Vt = V2 - Z2*I = 415+j0 - (0+j6)(-41.5-j41.5) = 415+j0-(-j249-249j^2) as j^2 = -1 then:
Vt = 415-(249-j249) = 166+j249V
ZL = 50@0.7lag = 50∠-45.572998 = 35+j35.70714Ω
Zt = j4in parallel with j6= j2.4
so load current:
I = V / ZL + Zt = 166+j249 / ( 0+j2.4 + 35+j35.70714 ) = 166+j249 / 35+j38.10714
this as a polar division I = 299.26∠56.310 / 51.741∠47.434 = 5.784∠8.876A
I have only completed part (a), once I know I'm on the right track I'll complete b & c. All help is greatly appreciated as always.