- #1
xortan
- 78
- 1
Hello,
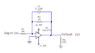
I am designing an op-amp to be used as a low-pass filter and am using a TLC271. I have attached an image of the topology of the circuit. I found the transfer function to be G(s) = Y(s)/X(s) = 1/(10^-4s + 1).
I plotted the bode plot in MATLAB and have attached the result in the second figure. However when looking at the datasheet there is a graph that shows how the phase and gain will change with frequency. (Also included this image)
How can I determine the frequency dependent gain and phase shifting of TLC271 on the frequency response of the circuit?
Thanks!
I am designing an op-amp to be used as a low-pass filter and am using a TLC271. I have attached an image of the topology of the circuit. I found the transfer function to be G(s) = Y(s)/X(s) = 1/(10^-4s + 1).
I plotted the bode plot in MATLAB and have attached the result in the second figure. However when looking at the datasheet there is a graph that shows how the phase and gain will change with frequency. (Also included this image)
How can I determine the frequency dependent gain and phase shifting of TLC271 on the frequency response of the circuit?
Thanks!