Magnetic field in an offset hole in a conductor cylinder

[zweebna]

Homework Statement

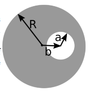
A long (infinite) wire (cylindrical conductor of radius R, whose axis coincides with the z axis carries a uniformly distributed current I in the +z direction. A cylindrical hole is drilled out of the conductor,
parallel to the z axis, (see figure above for geometry). The center of the hole is at x = b , and the radius of the hole is a. Determine the magnetic field in the hole region.

Homework Equations

$\oint B \cdot dl = \mu_0 I_\text{enc}$

The Attempt at a Solution

I'm pretty sure that I have the magnitude of the field, but I'm unsure how to get the direction. For the magnitude, I took a superposition of a cylinder with current density $J$ and a cylinder of current density $-J$ where the hole is. The magnitude of the magnetic field of each cylinder is $$B_1=\frac{\mu_0 J}{2}s_1 $$ and $$B_2=- \frac{\mu_0 J}{2}s_2 $$ respectively. Adding magnitudes together gives $$B_1+B_2=\frac{\mu_0 J}{2}(s_1-s_2)$$ and since $s_1-s_2 = b$ and $J=\frac{I}{2 \pi (R^2-a^2)}$ for the magnitude in the hole I get $$B_1+B_2=\frac{\mu_0 I b}{2 \pi (R^2-a^2)}$$
My professor said it would be easier to find the direction if I convert to cartesian coordinates, but my book says that the $\hat{s}$ direction in cartesian coordinates is $cos\phi \hat{x} +sin \phi \hat{y}$ but that would seem to give $$B_1+B_2=\frac{\mu_0 I b}{2 \pi (R^2-a^2)} (cos\phi \hat{x} +sin \phi \hat{y})$$ which definitely does not make sense.

 

[marcusl]

I'm not sure what s is. Your expressions for B should be involve the radii a and b. As for direction, write B as a vector instead, starting with Ampere's law written properly as $$\oint{\vec B \cdot \vec{dl}}=\mu_0 I_{enc}.$$Think about what contour you use in the integral, and what direction $\vec B$ takes along that contour.