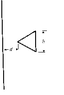Magnetic flux through a triangular loop?

[Abdulwahab Hajar]

Homework Statement

Determine the mutual inductance between a very long, straight wire and a conducting equilateral triangular loop

Homework Equations

I know how to do it but I'm stuck at the step of finding the total inductance through the triange.

The Attempt at a Solution

we know that the magnetic field due to an infinitely long wire is
B = µI/2πr
in order to find the magnetic flux through the triangle we need to find Φ = ∫B.dA
we have B but what would dA be in this case
the book says it's (2/√3) * (r - d) *dr
why is that so?

thank you

 

[RUber]

Look at the geometry for your triangle.
Starting at the point closest to the wire, we will call that $(d, 0)$ , you will follow a counterclockwise path to $(d+\frac{b\sqrt{3}}{2}, -\frac b2 )$, then from
$(d+\frac{b\sqrt{3}}{2}, -\frac b2 )$ to $(d+\frac{b\sqrt{3}}{2}, +\frac b2 )$, and finally from $(d+\frac{b\sqrt{3}}{2}, +\frac b2 )$ to $(d,0 )$.
Of course, you can parameterize each of those line integrals to get a form that is easier to work with.

 

[Abdulwahab Hajar]

Look at the geometry for your triangle.
Starting at the point closest to the wire, we will call that $(d, 0)$ , you will follow a counterclockwise path to $(d+\frac{b\sqrt{3}}{2}, -\frac b2 )$, then from
$(d+\frac{b\sqrt{3}}{2}, -\frac b2 )$ to $(d+\frac{b\sqrt{3}}{2}, +\frac b2 )$, and finally from $(d+\frac{b\sqrt{3}}{2}, +\frac b2 )$ to $(d,0 )$.
Of course, you can parameterize each of those line integrals to get a form that is easier to work with.

Ok that really helped to be honest.
Thank you sir
But that would be a line integral right?
what if I wanted to cover the surface as in the area covered by the sides of the triangle

 

[RUber]

Then, in that case, you would have x going from d to d+b/2 * sqrt(3) and y ranging from the lower line to the upper line (as a function of x).
These bounds are no fun to work with, but will get you to the answer for the surface integral.

 

[Abdulwahab Hajar]

Then, in that case, you would have x going from d to d+b/2 * sqrt(3) and y ranging from the lower line to the upper line (as a function of x).
These bounds are no fun to work with, but will get you to the answer for the surface integral.

Yeah I get ya...
is there anyway to do it with a change in r since it covers both x and y directions...
this is how it is in the solution manual perhaps if you take a look you could understand how it was derived
I just couldn't figure it out

 

[RUber]

I see what they did there. Since the wire in infinitely long, B is only dependent on r, the distance from the line.
So, if you slice up the equilateral triangle vertically, along lines with the same distance to the wire, you get
$\int\int B \, dA = \int B h(r) dr,$
where $h(r)$ is the height of the triangle at distance r.
At r=d, the height is 0, and at r = $d+b\sqrt{3}/2$, the height is b. So you can make a linear rule for the height that looks like
$h = (r-d)\frac{2}{\sqrt{3}} .$
Check that against the reference points to make sure.
So, now you can treat the integral in terms of one variable, r.
$\int B h(r) dr = \int B (r-d)\frac{2}{\sqrt{3}}\, dr$
The final answer applies a simplification in the natural log, but otherwise, you should be able to follow the rest from there with about 2 extra steps.
I hope this helps.

 

[Abdulwahab Hajar]

I see what they did there. Since the wire in infinitely long, B is only dependent on r, the distance from the line.
So, if you slice up the equilateral triangle vertically, along lines with the same distance to the wire, you get
$\int\int B \, dA = \int B h(r) dr,$
where $h(r)$ is the height of the triangle at distance r.
At r=d, the height is 0, and at r = $d+b\sqrt{3}/2$, the height is b. So you can make a linear rule for the height that looks like
$h = (r-d)\frac{2}{\sqrt{3}} .$
Check that against the reference points to make sure.
So, now you can treat the integral in terms of one variable, r.
$\int B h(r) dr = \int B (r-d)\frac{2}{\sqrt{3}}\, dr$
The final answer applies a simplification in the natural log, but otherwise, you should be able to follow the rest from there with about 2 extra steps.
I hope this helps.

It's great man
Thanks a lot
You're the best