Magnetic force on triangular loop of wire

[rmiller70015]

Homework Statement

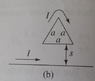
Find the force on the triangular loop in the figure:
I am trying to do this in cylindrical polar coordinates, because it builds character.

Homework Equations

$$\vec{B}(\vec{r}) = \frac{\mu _0}{4\pi} \int \frac{I(d\vec{l} \times \hat{\alpha})}{|\vec{\alpha}|^2}$$
Where alpha is the script r vector (I couldn't figure out how to do script r in mathjax).
and

$$\vec{F} = I\int (d\vec{I} \times \vec{B})$$

The Attempt at a Solution

I've found the magnetic field due to the lower wire by using the Biot-Savart law and an example in the book. It is $$\frac{\mu _0 I}{2s\pi} \hat{\phi}$$

The solution uses Cartesian coordinates to integrate along the two wires. I figure that the (x,y) coordinates would be the (z,s) coordinates from the way I set up my cylindrical system (+z is along the wire and +s is up).

The cross product is:
$$d\vec{l_A} \times \vec{B} = \begin{vmatrix} s & \phi & z \\ 0 & 0 & -dz \\ 0 & \frac{\mu _0 I}{2s\pi} & 0 \end{vmatrix} = \frac{\mu _0 I}{2s\pi}\hat{s} $$

Then the force is:
$$\vec{F_A} = I\int^{a}_{0}\frac{\mu _0 I}{2\pi}dz\hat{s} = \frac{\mu _0 I^2a}{2\pi}\hat{s}$$

Then, finding the cross product for the B and C lengths become more difficult because I'm not quite sure if I am using the correct directions and I'm unsure of my limits of integration.
$$ d\vec{l_B} \times \vec{B} = \begin{vmatrix} s & \phi & z \\ ds & 0 & dz \\ 0 & \frac{\mu _0 I}{2s\pi} & 0 \end{vmatrix} = -\frac{\mu _0 I}{2s\pi}dz\hat{s} + \frac{\mu _0 I}{2s\pi}ds\hat{z}$$

And the Force integral is:
$$\vec{F_B} = I\int-\frac{\mu _0 I}{2s\pi}dz\hat{s} + I\int \frac{\mu _0 I}{2s\pi}ds\hat{z}$$

Again I am uncertain if these integrals are correct and I'm unsure of the limits. I believe for dz differential I should be integrating between 0 and a. For the ds differential I should be integrating between s and √¾a. The integrals will give me a root3/2 and a natural log expression which are in the answer key, but I am not confident that what I am doing is correct.

 

[kuruman]

I figure that the (x,y) coordinates would be the (z,s)

Do yourself a favor. Don't use "s" as a variable because the symbol has been reserved as the fixed distance between the long wire and the base of the triangular loop. Call it something else, r is good if you insist on cylindrical coordinates.

 

[rmiller70015]

Do yourself a favor. Don't use "s" as a variable because the symbol has been reserved as the fixed distance between the long wire and the base of the triangular loop. Call it something else, r is good if you insist on cylindrical coordinates.

The book likes to call it s, so I went with that, but I think I see what you're saying. If I do that integral with respect to s, I might accidentally integrate it and the s should show up in the limits.

 

[kuruman]

If the book calls it "s" and you like it, then relabel in the figure the distance between the long wire and the base of the triangle something other than "s".