How Do You Calculate the Angular Motion of a Pulley System?

[ikihi]

Homework Statement

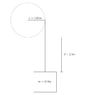
Consider a pulley with a mass-less cord attached to its edge. The rope hangs a distance of d= 2.50 m below the bottom of the pulley. Attached to the end of this cord is a block with mass 3.00 kg. There is also an electric motor attached to the pulley which supplies a torque of 28.7 N * m. The pulley can be considered a disk with a radius of 0.65 m. The mass of the pulley is 1.3 kg.

a) What is the torque due to the hanging block? Answer: 19.11 N ⋅ m
b) what is the moment of inertia of the pulley? Answer: 0.2746 kg ⋅ m
c) Once the motor is turned on the pulley begins to rotate counter clock-wise. What is the magnitude of the angular acceleration of the pulley? Answer: 6.22 rad/sec²
d) Through how many radians must the pulley rotate in order to lift the block to the bottom edge of the pulley?
e) Once the motor is turned on, how long will it take the top edge of the block to reach the bottom of the pulley?

Homework Equations

I = 0.5 * m * r^2 (moment of inertia)

The Attempt at a Solution

I need help with d and e.
[/B]
d) The circumference of the pulley is 4.08 m and the cord is 2.50 m. So the total rotation length is 1.58 m. How do i find how many revolutions from this? It should be less than 1 revolution, correct?

e) t = ± √(2⋅θ)/(α)
t = ?

 

[haruspex]

So the total rotation length is 1.58 m

I don't knowwhat you mean by rotation length. You seem to have divided circumference by rope length, but that will not give a distance.
If the disc were to rotate one revolution, it would haul the rope up 4.08m. How many radians is one revolution? What fraction of that would haul it up the desired distance?

 

[ikihi]

I don't knowwhat you mean by rotation length. You seem to have divided circumference by rope length, but that will not give a distance.
If the disc were to rotate one revolution, it would haul the rope up 4.08m. How many radians is one revolution? What fraction of that would haul it up the desired distance?

There are 2π radians in one revolution. So if i take 2.50m/4.08 m that is 0.613 rad?(not sure on the equation to use here) If I take 0.613 rad/2π = 0.963 revolutions? (The equation I used here was n= θ/2π)

 

[haruspex]

There are 2π radians in one revolution. So if i take 2.50m/4.80 m that is 0.613 rad. If I take 0.613 rad/2π = 0.963 revolutions? (The equation I used was n= θ/2π)

No, I think you have done the conversion backwards. Better to keep things symbolic as long as possible, so let the radius be r.
One revolution would haul 2πr. To haul length L, what fraction of a revolution is that?

 

[ikihi]

No, I think you have done the conversion backwards. Better to keep things symbolic as long as possible, so let the radius be r.
One revolution would haul 2πr. To haul length L, what fraction of a revolution is that?

0.61213

 

[haruspex]

0.61213

I said to keep everything symbolic. Ignore the given numbers. Express it in terms of r, L etc.

 

[ikihi]

I said to keep everything symbolic. Ignore the given numbers. Express it in terms of r, L etc.

L = d / 2⋅π⋅r

 

[haruspex]

L = d / 2⋅π⋅r

What is d? I defined L as the length of rope. I did not define a variable for the fraction, but let's call it f.

 

[ikihi]

What is d? I defined L as the length of rope. I did not define a variable for the fraction, but let's call it f.

f = L / 2⋅π⋅r

so... f = 2.50m / 2⋅π⋅0.65 m = 0.61213

 

[haruspex]

f = L / 2⋅π⋅r

Right. That is a fraction of a revolution, remember. How many radians is one revolution?

 

[ikihi]

Right. That is a fraction of a revolution, remember. How many radians is one revolution?

There is 2π rad/rev or 6.28319 rad/rev.
So you are saying it is 0.61213 rev ⋅ 6.28319 rad/rev = 3.846 rad?

So how do i find how many revolutions? Is it n= θ rad / 2π rad ?

 

[haruspex]

There is 2π rad/rev

Right, so how many radians does a wheel of radius r need to turn to haul a length L?
(Please do not keep substituting numbers from the actual question. Keep it symbolic for now.)

 

[ikihi]

Right, so how many radians does a wheel of radius r need to turn to haul a length L?
(Please do not keep substituting numbers from the actual question. Keep it symbolic for now.)

A fractional amount of 2π rad/rev.

f * 2π = L / r

 

[haruspex]

A fractional amount of 2π rad/rev.

f * 2π = L / r

Right. Do you see now why I pushed you to work symbolically? The πs cancelled, leaving a very simple formula for the number of radians.

 

[ikihi]

Right. Do you see now why I pushed you to work symbolically? The πs cancelled, leaving a very simple formula for the number of radians.

I understand your reasoning, but I still am confused. which two π canceled? What variable am I solving for in that formula f * 2π = L / r ?

 

[haruspex]

I understand your reasoning, but I still am confused. which two π canceled? What variable am I solving for in that formula f * 2π = L / r ?

d) asked for the number of radians. You have found it be be L/r. There was no need to do any calculations involving π since it canceled out.