- #1
skrat
- 748
- 8
Homework Statement
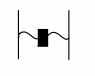
We have two springs each ##0.5 m## long and both have ##k=5N/cm##. One end of the spring is attached to the wall while the other two ends are connected in the middle. On the junction point of the two springs a mass is hanged. How does the frequency of oscillation around equilibrium state depend on the initial offset due to the mass?
Hint: There is no need to explicitly write the initial offset as function of mass. Just use the offset as independent parameter using which mass can be calculated.
Homework Equations
The Attempt at a Solution
##mg+2Fsin\varphi=ma##
##mg+2k\frac{z}{\sqrt{l^2+z^2}}(\sqrt{l^2+z^2}-l)=m\ddot{z}##
Let's say that ##z=D+\varepsilon ## where ##\varepsilon ## is very small.
##mg+2k\frac{D+\varepsilon }{\sqrt{l^2+(D+\varepsilon )^2}}(\sqrt{l^2+(D+\varepsilon )^2}-l)=m\ddot{\varepsilon }##
##mg+2k(D+\varepsilon)-\frac{2kl(D+\varepsilon )}{l\sqrt{1+(\frac{D+\varepsilon }{l})^2}}=m\ddot{\varepsilon }##
##mg+2k(D+\varepsilon )-2k(D+\varepsilon)[1-\frac 1 2 (\frac{D+\varepsilon }{l})^2]=m\ddot{\varepsilon }##
##mg+\frac{2k}{l^2}(D+\varepsilon )^3=m\ddot{\varepsilon }##
##mg+\frac{2kD^3}{l^2}[1-3\frac \varepsilon D]=m\ddot{\varepsilon }##
##\ddot{\varepsilon }+\frac{6kD^2}{ml^2}\varepsilon =g+\frac{2kD^3}{l^2}##
So if I am not mistaken, than ##\omega \propto D##. Right?