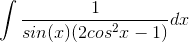SUMMARY
The discussion focuses on techniques for solving tricky trigonometric integrals, specifically using universal substitution and trigonometric identities. The method involves replacing the constant 1 in the numerator with the identity sin²(x) + cos²(x), which simplifies the integration process. This approach allows for the integral to be expressed in a more manageable form, ultimately leading to a solution by integrating simpler terms. The participants confirm the effectiveness of this method in achieving the desired results.
PREREQUISITES
- Understanding of trigonometric identities, specifically sin²(x) + cos²(x)
- Familiarity with integration techniques, including universal substitution
- Knowledge of derivatives of trigonometric functions
- Ability to manipulate algebraic expressions involving trigonometric functions
NEXT STEPS
- Study advanced integration techniques, focusing on trigonometric integrals
- Learn about the application of universal substitution in calculus
- Explore the use of trigonometric identities in simplifying integrals
- Practice solving complex integrals involving sin(x) and cos(x)
USEFUL FOR
Students and professionals in mathematics, particularly those studying calculus and integration techniques, as well as educators looking for effective methods to teach trigonometric integrals.