Math Challenge by Andrewkirk #1

[Greg Bernhardt]

Submitted and judged by: @andrewkirk
Solution credit:

RULES:
1) In order for a solution to count, a full derivation or proof must be given. Answers with no proof will be ignored.
2) It is fine to use nontrivial results without proof as long as you cite them and as long as it is "common knowledge to all mathematicians". Whether the latter is satisfied will be decided on a case-by-case basis.
3) If you have seen the problem before and remember the solution, you cannot participate in the solution to that problem.
4) You are allowed to use google, wolframalpha or any other resource. However, you are not allowed to search the question directly. So if the question was to solve an integral, you are allowed to obtain numerical answers from software, you are allowed to search for useful integration techniques, but you cannot type in the integral in wolframalpha to see its solution.

CHALLENGE:
A triangle has vertices $A$, $B$ and $C$. Mark points $A',B',C'$ on edges $\overline{BC},\overline{CA},\overline{AB}$ respectively so that each is one third of the way along the edge, as shown in the diagram. The lines $\overline{AA'},\overline{BB'},\overline{CC'}$ intersect at points $A'',B'',C''$ and form a triangle inside triangle $ABC$.

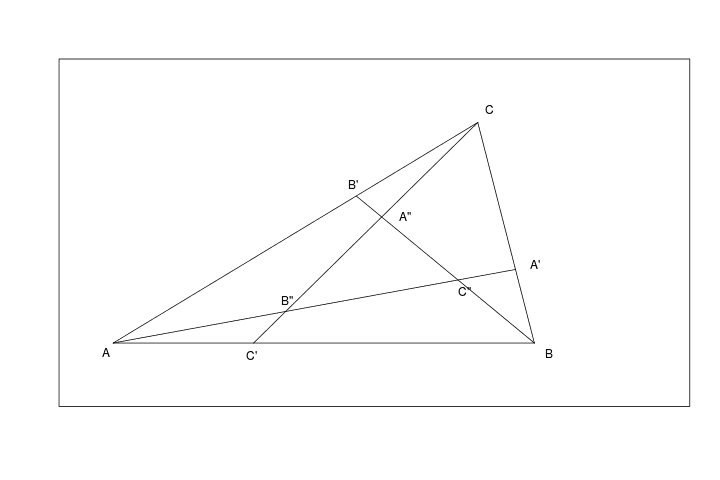
Find a formula for the ratio of the area of triangle $A''B''C''$ to that of triangle $ABC$ in terms of the side lengths and/or angles of the latter. Does this formula vary with the shape of the triangle?

There are different possible approaches to the derivation of a formula:

1. Using only Euclidean techniques: similar triangles, opposite and corresponding angles etc
2. Using trigonometry
3. Using coordinate geometry
4. Another technique that gives a particularly neat derivation, which I won't give away other than to say it requires embedding the triangle in three-dimensional space.

 

[zwierz]

One just should present each of vectors $\boldsymbol {A''B''}$ and $\boldsymbol{A''C''}$ as a linear combination of vectors $\boldsymbol {AB}$, $\boldsymbol{AC}$ (just do not introduce Cartesian frame for that!). And obtain then an equation $\boldsymbol {A''B''}\times \boldsymbol{A''C''}=const (\boldsymbol {AB}\times \boldsymbol{AC}).$ Quite standard task I guess.

You can also find a ratio of volumes of two tetrahedrons if for example vertices of one tetrahedron lie on intersections of medians of faces of another tetrahedron.

 

[zwierz]

why has nobody still written the answer? Let's begin. Let's use vectors $\boldsymbol{AB},\boldsymbol{AC}$ as a basis.
Line $CC'$ has the equation
$$\boldsymbol r_{CC'}=\boldsymbol {AC}+t(\boldsymbol{AB}/3-\boldsymbol{AC});\quad t\in\mathbb{R}$$
Line $AA'$ has the equation
$$\boldsymbol r_{AA'}=s\big(\boldsymbol{AB}+(\boldsymbol{AC}-\boldsymbol{AB})/3\big),\quad s\in\mathbb{R}$$
To find $B''$ one must solve the equation $\boldsymbol r_{CC'}=\boldsymbol r_{AA'}$. From this equation we have
$$t=6/7,\quad s=3/7$$
so that $\boldsymbol {AB''}=\boldsymbol{AC}/7+2\boldsymbol{AB}/7$

go on $\boldsymbol{AC''}=?,\quad \boldsymbol{AA''}=?$

 

[QuantumQuest]

As we have to do with three non - concurrent cevians in this problem (namely $AA^{\prime}, BB^{\prime}, CC^{\prime}$), we will utilize Routh's Theorem - for a proof using Menelaus Theorem see for example Wikipedia.[/PLAIN]

Using the diagram given in the problem, Routh's Theorem states that if points $A^{\prime}, B^{\prime}, C^{\prime}$ lie on the segments $BC, CA$ and $AB$ then writing $\frac{CA^{\prime}}{BA^{\prime}} = x, \frac{AB^{\prime}}{CB^{\prime}} = y, \frac{BC^{\prime}}{AC^{\prime}} = z$ the area of the triangle formed by the cevians $AA^{\prime}, BB^{\prime}, CC^{\prime}$ (i.e. triangle $A^{\prime\prime}B^{\prime\prime}C^{\prime\prime}$) is the area of the triangle $ABC$ times $\frac{(xyz - 1)^2}{(xy + y +1)(yz + z +1)(zx + x + 1)}$.

Using the above formula in the context of our problem we have: $\frac{(xyz - 1)^2}{(xy + y +1)(yz + z +1)(zx + x + 1)} = \frac{(2\cdot2\cdot2- 1)^2}{(2\cdot2 + 2 + 1)(2\cdot2 + 2 +1)(2\cdot2 + 2 + 1)} = \frac{7^2}{7^3} = \frac{1}{7}$. This is known as the one - seventh area triangle.

Due to the generality of Routh's Theorem the formula holds for any shape of triangle.

 

[zwierz]

Wow! thus this so called Featured Challenge is even a direct consequence of the known result. What a sad story is this

 

[QuantumQuest]

Wow! thus this so called Featured Challenge is even a direct consequence of the known result. What a sad story is this

Let me clear things up a little bit. I chose to go with cevians in my solution so because they were not concurrent, they form a internal triangle and there is Routh's Theorem that is an already known result. If there weren't a such theorem, I'd had essentially to move through the steps of its proof. For anyone going some other way to solve the problem, there are other things to consider and take into account. The problem is very interesting and there are many ways to tackle it. So, in conclusion, the only sad story I see here is the wrong impressions you try to give.

 

[andrewkirk]

As we have to do with three non - concurrent cevians in this problem (namely $AA^{\prime}, BB^{\prime}, CC^{\prime}$), we will utilize Routh's Theorem - for a proof using Menelaus Theorem see for example Wikipedia.[/PLAIN]

Using the diagram given in the problem, Routh's Theorem states that if points $A^{\prime}, B^{\prime}, C^{\prime}$ lie on the segments $BC, CA$ and $AB$ then writing $\frac{CA^{\prime}}{BA^{\prime}} = x, \frac{AB^{\prime}}{CB^{\prime}} = y, \frac{BC^{\prime}}{AC^{\prime}} = z$ the area of the triangle formed by the cevians $AA^{\prime}, BB^{\prime}, CC^{\prime}$ (i.e. triangle $A^{\prime\prime}B^{\prime\prime}C^{\prime\prime}$) is the area of the triangle $ABC$ times $\frac{(xyz - 1)^2}{(xy + y +1)(yz + z +1)(zx + x + 1)}$.

Using the above formula in the context of our problem we have: $\frac{(xyz - 1)^2}{(xy + y +1)(yz + z +1)(zx + x + 1)} = \frac{(2\cdot2\cdot2- 1)^2}{(2\cdot2 + 2 + 1)(2\cdot2 + 2 +1)(2\cdot2 + 2 + 1)} = \frac{7^2}{7^3} = \frac{1}{7}$. This is known as the one - seventh area triangle.

Due to the generality of Routh's Theorem the formula holds for any shape of triangle.

That looks good QQ. I had not heard of that theorem. You have a more compendious knowledge of geometric theorems than I!

I've looked at the wiki proof of Routh's theorem. The last step is accompanied by no justification. At worst, one would have to expand the expressions over a common denominator to get 54 terms in the numerator, which one would then need to collapse via cancellation to (hopefully) eventually get the four terms necessary to make the final numerator $(xyz-1)^2$

Are you able to find an elegant way to justify that final step?

 

[QuantumQuest]

Are you able to find an elegant way to justify that final step?

I cannot really see any purely algebraic noteworthy way / trick that works in an overall way to save the burden of doing the math, as cyclic transformations / substitutions / eliminations have certain issues, due to the specific form of the fractions. Anyway, I did the math and the result is correct but it is very long and burdensome. But it will be very interesting if anyone comes up with some neat trick.

 

[andrewkirk]

I cannot really see any purely algebraic noteworthy way / trick that works in an overall way to save the burden of doing the math, as cyclic transformations / substitutions / eliminations have certain issues, due to the specific form of the fractions. Anyway, I did the math and the result is correct but it is very long and burdensome. But it will be very interesting if anyone comes up with some neat trick.

Well done! You have more patience than me . I couldn't bring myself to go through it, as I'd most likely get a sign wrong somewhere and then the thing wouldn't cancel and collapse down properly. I thought I could glimpse a shortcut that used symmetries between the ways the three variables appear in the expressions, but I didn't end up with a usable argument.

I have been test-driving a symbolic algebra program called Maxima - a free open-source analogue of Maple, though I expect not as powerful. I typed the difference of the two expressions into it and asked it to expand and then simplify, and was gratified to see it said the answer was zero. This encourages me to start investing a little time in learning to use a package like that - maybe even paying for a full-powered one like Maple or Mathematica - as it looks like it would be useful in working on big messy expressions like this. The Holy Grail for me would be to be able to shortcut calculations of Einstein tensors in GR - eg for the Schwarzschild or FLRW metrics - as that is so laborious yet repetitive.